Matrizes: Multiplicação de matriz por escalar

Seja um número k ∈ ℝ, e uma matriz A = (aij)_m×n, o produto k · A é a matriz B = (bij)_m×n obtida multiplicando-se cada elemento de A por k, isto é, bij = k · aij para todo i e todo j.

PROPRIEDADES

Sejam A e B matrizes m×n e a,b∈ℝ.

a. 1· A =A
b. (-1) ·A = -A
c. a · 0_m×n = 0_m×n
d. 0 · A = 0_m×n
e. a · (A + B) = a · A + a · B
f. (a + b) · A = a · A + b · A
g. a · (b · A) = (ab) · A

MULTIPLICAÇÃO DE MATRIZES

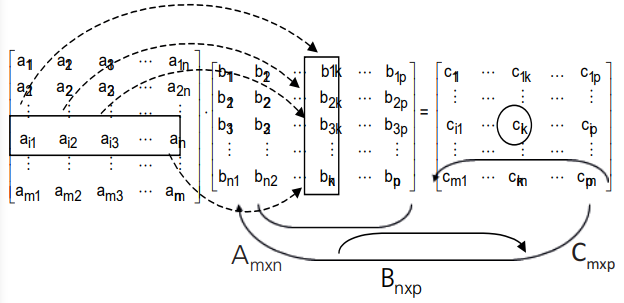
Sejam duas matrizes A = (aij)_m×n e B = (bjk)_n×p, o produto de A por B, A · B, é a matriz m × p, C = (cik)_m×p, onde o elemento C_ik localizado na i-ésima linha e k-ésima coluna, é obtido multiplicando-se os elementos da i-ésima linha de A pelos correspondentes elementos da k-ésima coluna de B e somando os produtos parciais assim obtidos.

c_ik = a_i1b_1k + a_i2b_2k + a_i3b_3k+…+ a_inb_nk = ∑ⁿ_{j =1} a_ij · b_jk

Considerando as linhas da matriz A e as colunas da matriz B como vetores no Rⁿ, cada elemento cik é obtido pelo produto escalar do i-ésimo vetor linha de A pelo k-ésimo vetor coluna de B.

O produto de duas matrizes AB somente existe quando A possui tantas colunas quantas são as linhas de B. Nesse caso, diz-se que as duas matrizes A e B são conformáveis para a multiplicação.

O produto AB é uma matriz que possui o número de linhas de A e o número de colunas de B.

c_ik = a_ikb_1k + a_i2b_2k + a_i3b_3k + … + a_inb_nk

Exemplo:

PROPRIEDADES

a. A multiplicação de matrizes não é comutativa, isto é, para duas matrizes quaisquer A e B é falso que AB = BA necessariamente.

1º CASO: AB existe e BA não existe:

m≠p ⇒ A_m×n · B_n×p = AB_m×p ⇒ B_nxp · A_m×n ⇒ ∄BA

2º CASO: AB e BA existem, mas são de tipos diferentes

A_m×n · B_n×m = AB_m×m
B_n×m · A_m×n = BA_n×n

3º CASO: AB e BA existe e são do mesmo tipo (A e B são matrizes quadradas de mesma ordem), mesmo assim em geral temos AB ≠ BA.

4º CASO: Sejam A e B matrizes quadradas e de mesma ordem, quando ocorre AB = BA, diz-se que A e B comutam.

a. Associatividade: (A · B) · C = A · (B · C) 
b. Distributividade em relação à adição: A · (B + C) = A · B + A · C ⇔ A · (B + C) = A · B + A · C
c. (k · A) · B = A · (k · B) = k · (A · B)
d. Elemento Neutro: A_m×n . I_n = I_m . A_m×n = A_m×n

f. Multiplicação pela matriz nula:
0_p×m · A_m×n = 0_p×n
A_m×n · 0_n×p = 0_m×p

Observação:

1. Sendo A·B=0 não se pode concluir que A = 0 ou B = 0. Veja o seguinte exemplo onde A ≠ 0,B ≠ 0 e AB = 0.

2. Quando temos A · B = A · C ou (B · A = C · A) não se pode concluir que B = C, mesmo que A ≠ 0. Veja o exemplo a seguir, onde tem-se AB = AC e B ≠ C.

3. (A + B)² = A² + AB + BA + B²