Uma matriz de ordem m×n , M = (ai)m×n‘ é uma lista de números aij, onde 1 ≤ i ≤ m e 1 ≤ j ≤ n, dispostos em m linhas e n colunas, na qual o elemento aij está localizado no cruzamento da i-ésima linha com a j-ésima coluna.

Os elementos que possuem o mesmo 1º índice encontram-se na mesma linha e os que possuem o mesmo 2º índice encontram-se na mesma coluna.
A lista ordenada (ai1, ai2 ,…, ain) chama-se i-ésima linha ou i-ésimo vetor-linha da matriz. A lista ordenada (a1j, a2j,…,amj) chama-se j-ésima coluna ou j-ésimo vetor-coluna da matriz. Assim, as linhas de uma matriz m×n são vetores do Rn e as colunas, vetores do Rm.
O número de elementos que constituem a matriz m×n é m·n.
Assim, a matriz 2×3 abaixo possui 2 linhas e 3 colunas e um total de 6 elementos.

Podemos identificar os elementos a11 = 1, a12 = 2, a13 = 3, a21 = -3, a22 = -2 e a23 = -1.
A matriz constituída pelo mesmo número de linhas e colunas é chamada matriz quadrada. Assim, uma matriz constituída por $\mathrm{n}$ linhas e $n$ colunas é uma matriz quadrada de ordem $n \times n$ ou simplesmente uma matriz quadrada de ordem $\mathbf{n}$.
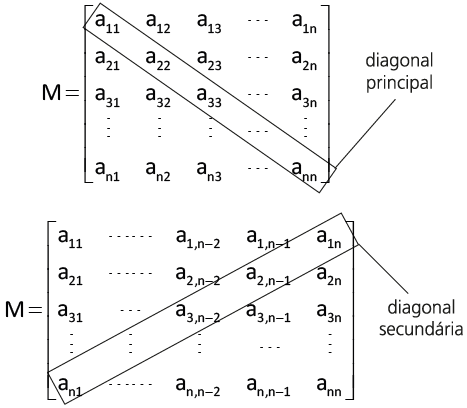
Em uma matriz quadrada de ordem $n$, o conjunto dos elementos $a_{\mathrm{ij}}$ tais que:
a . i = j chama-se diagonal principal;
b . i +j = n + 1 chama-se diagonal secundária.