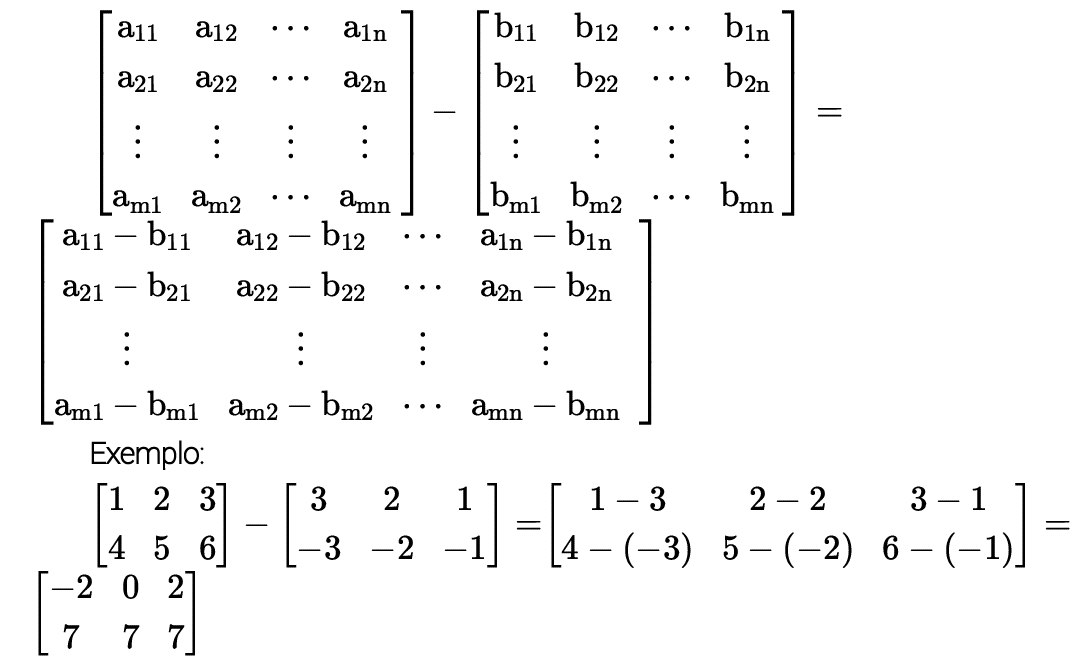
IGUALDADE DE MATRIZES
Duas matrizes são iguais se, e somente se, possuem a mesma ordem e todos os elementos correspondentes (elementos com índices iguais, “i”, é, que ocupam a mesma posição) são iguais.
Sejam A = (aij)m×n e B = (bij)p×q , então
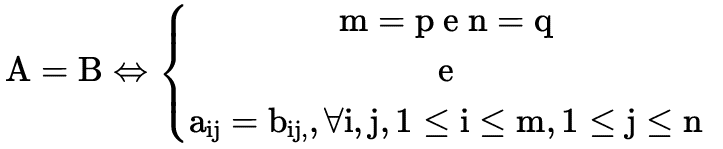
ADIÇÃO E SUBTRAÇÃO DE MATRIZES
Sejam as matrizes A e B de mesma ordem m×n, chama-se soma de A com B à matriz C=A+B, de ordem m×n, cujos elementos são obtidos somando-se os elementos correspondentes da matrizes A e B.
Sejam A = (aij)m×n e B = (bij)m×n então C = A + B é tal que:
C = (cij)m×n onde cij = aij + bij, ∀i, j, 1 ≤ i ≤ m e 1≤ j ≤ n

A adição de duas matrizes só é definida quando elas possuem a mesma ordem. Nesse caso, diz-se que elas são conformáveis para adição.
Exemplo:
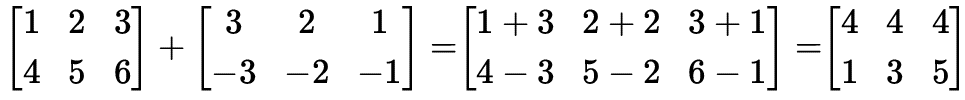
PROPRIEDADES DA ADIÇÃO
a) COMUTATIVA: A + B = B + A
b) ASSOCIATIVA: (A + B) + C = A + (B + C)
c) ELEMENTO NEUTRO: A + 0 =A onde 0 é a matriz nula da mesma ordem de A e possui todos os seus elementos nulos.
d) MATRIZ OPOSTA: A + (− A) = 0, onde −A é uma matriz da mesma ordem de A e cujos elementos são opostos dos elementos correspondentes de A.
Dadas A e B duas matrizes de mesma ordem, a diferença das matrizes A-B é definida como A-B=A+(-B).
Sendo A = (aij)m×n e B = (bij)m×n então D=A-B é tal que:
D = (dij)m×n , onde dij = aij – bijj , ∀i, j, 1 ≤ i ≤ m e 1 ≤ j ≤ n