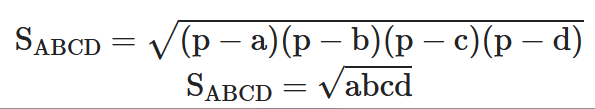Quadriláteros

QUADRADO

A área do quadrado é igual ao seu lado elevado ao quadrado.

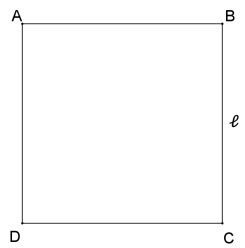
Seja ℓ o lado do quadrado ABCD, então sua área é S_ABCD = ℓ².

Demonstração:

Basta utilizar a expressão da área do retângulo onde a base e a altura são ambas iguais a ℓ. Assim, S_ABCD = ℓ ⋅ ℓ = ℓ².

LOSANGO

A área do losango é igual à metade do produto de suas diagonais.

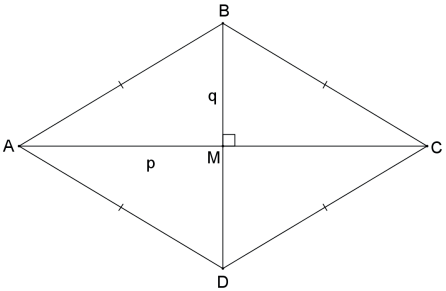
Seja o losango ABCD de diagonais AC = p e BD=q, então sua área é S_ABCD = ^p⋅q/₂.

Demonstração:

Inicialmente, cabe observar que o losango possui diagonais perpendiculares. Assim,

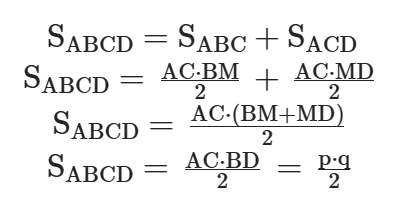
TRAPÉZIO

A área do trapézio é igual ao produto da semissoma de suas bases pela sua altura.

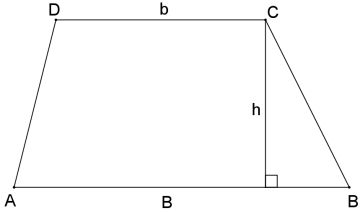
Seja o trapézio ABCD de bases AB = B e CD = b, e altura h, então sua área é S = ^B+b/₂ ⋅ h.

Demonstração:

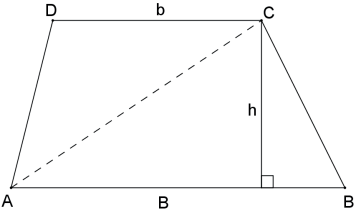
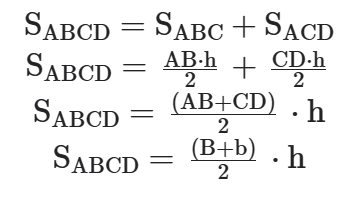
ÁREA DO QUADRILÁTERO CONVEXO

A área do quadrilátero convexo é igual à metade do produto das diagonais vezes o seno do ângulo entre as diagonais.

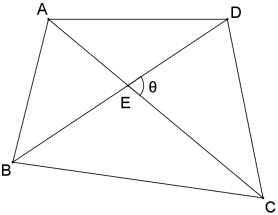
Seja um quadrilátero convexo cujo ângulo entre as diagonais AC=p e BD = q é igual a θ, então a área do quadrilátero é S = ^pq/₂ ⋅ sen θ.

Demonstração:

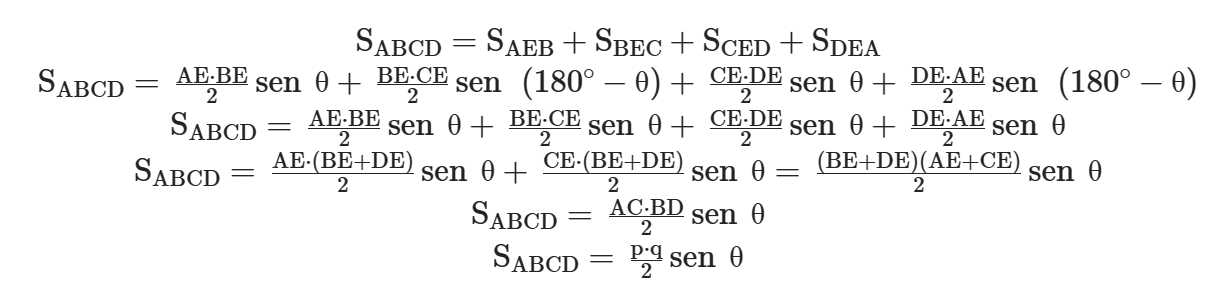
QUADRILÁTERO CIRCUNSCRITÍVEL

A área do quadrilátero circunscritível é igual ao produto do seu semiperímetro pelo raio do círculo inscrito.

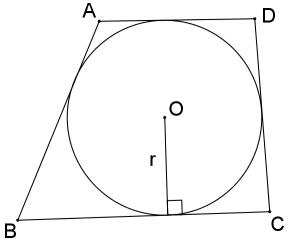
Seja o quadrilátero circunscritível ABCD, cujo semiperímetro é p = ^a+b+c+d/₂, então sua área é S_ABCD = p . r.

Demonstração:

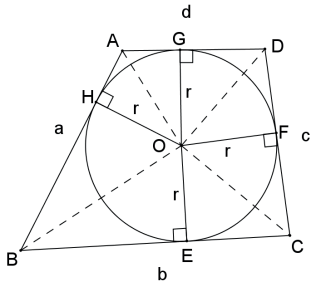
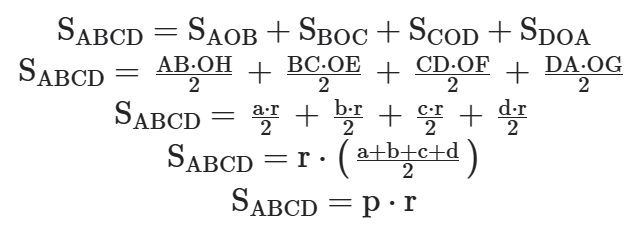
Note que essa propriedade é válida para qualquer polígono circunscritível.

QUADRILÁTERO INSCRITÍVEL

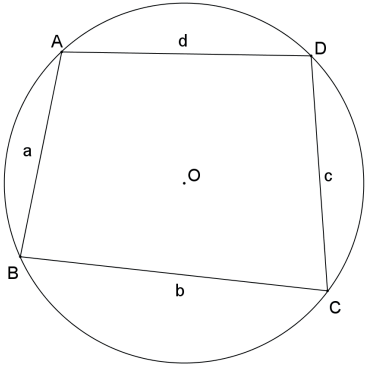
Seja o quadrilátero inscritível ABCD de lados AB = a, BC = b, CD = c e DA = d, e semiperímetro p = ^a+b+c+d/₂, então sua área:

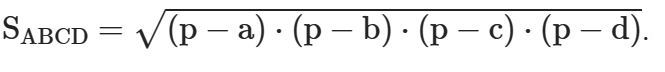
Demonstração:

Aplicando a lei dos cossenos no ΔABD, temos:

BD2 = a² + d² − 2ad ⋅ cos A^    (*)

Aplicando a lei dos cossenos no ΔBCD, temos:

BD² = b² +c² − 2bc . cos C^    (**)

Como o #ABCD é inscritível, então Â + C^{^} = 180° ⇒ cos C^{^} = −cos Â ∧ sen C^{^} = sen Â.

Igualando (*) e (**), temos:

QUADRILÁTERO INSCRITÍVEL E CIRCUNSCRITÍVEL

A área do quadrilátero inscritível e circunscritível é igual à raiz quadrada do produto dos seus lados.

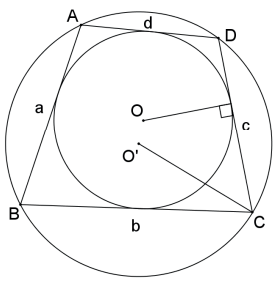
Seja o quadrilátero inscritível e circunscritível ABCD de lados AB = a, BC = b, CD = c e DA = d, então sua área é:

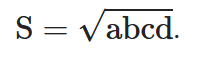
Demonstração:

Como o #ABCD é circunscritível, então, pelo teorema de Pitot, temos: a + c = b + d = p. Assim, a = p − c, c = p − a, b = p − d e d = p − b.

Utilizando a fórmula para o cálculo da área do quadrilátero inscritível, temos: