Vimos na resolução de uma equação do 2° grau que se o discriminante é negativo, ela não admite raízes reais. Por exemplo, a equação: x2 + 9 = 0 não admite raízes reais. Se usarmos os métodos que conhecemos para resolvê-la, obtemos: x2 = – 9 ⇒ x = ± √-9 mas é inaceitável tal resultado para x; os números negativos não têm raiz quadrada.
Para superar tal impossibilidade e poder, então, resolver todas equações do 2° grau, os matemáticos ampliaram o sistema de números, inventando os números complexos.
Primeiro, eles definiram um novo número i = √-1.
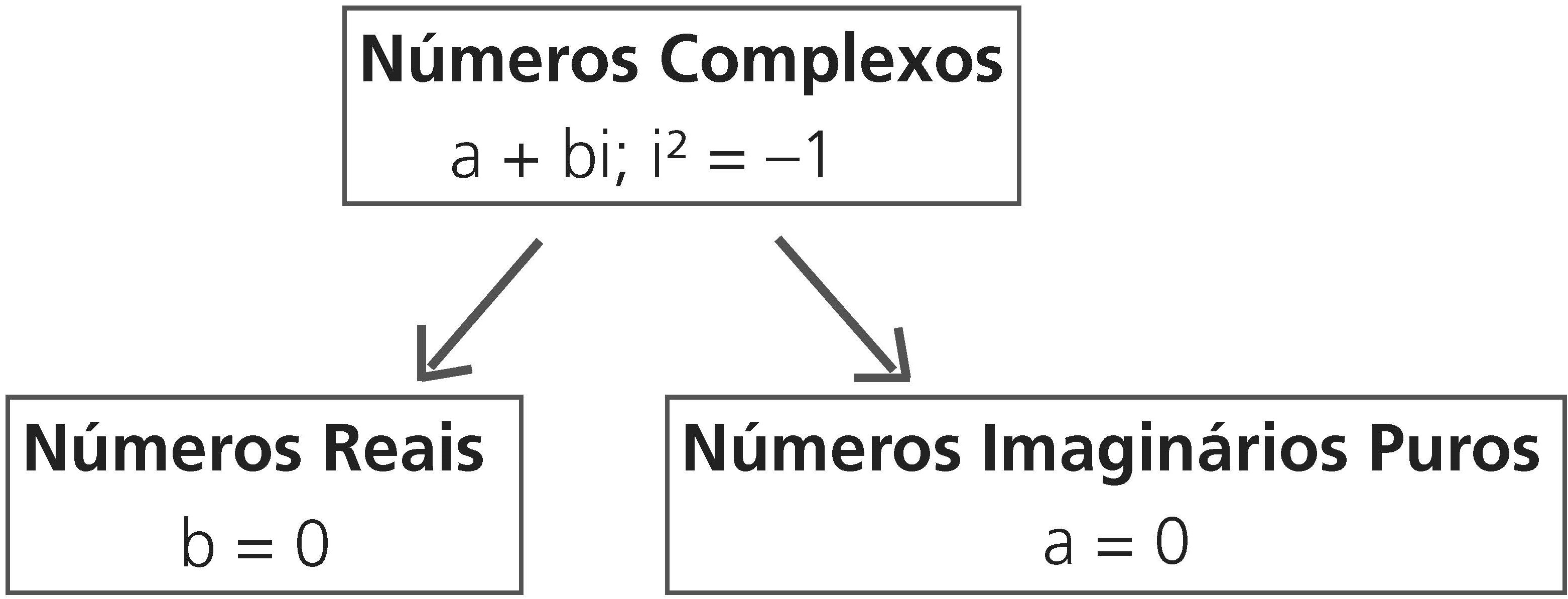
Isso conduz ai2=-1. Um número complexo é então um número da forma a+ bi onde a e b são números reais.
Para a equação acima fazemos
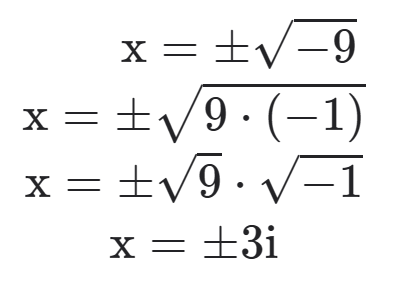
As raízes da equação x2 + 9 = 0 são 3i e -3 i.
DEFINIÇÃO
Um número complexo é uma expressão da forma a + bi, onde a e b são números reais i2 = -1. No número complexo a + bi, a é a parte real e b é a parte imaginária.
Exemplos:
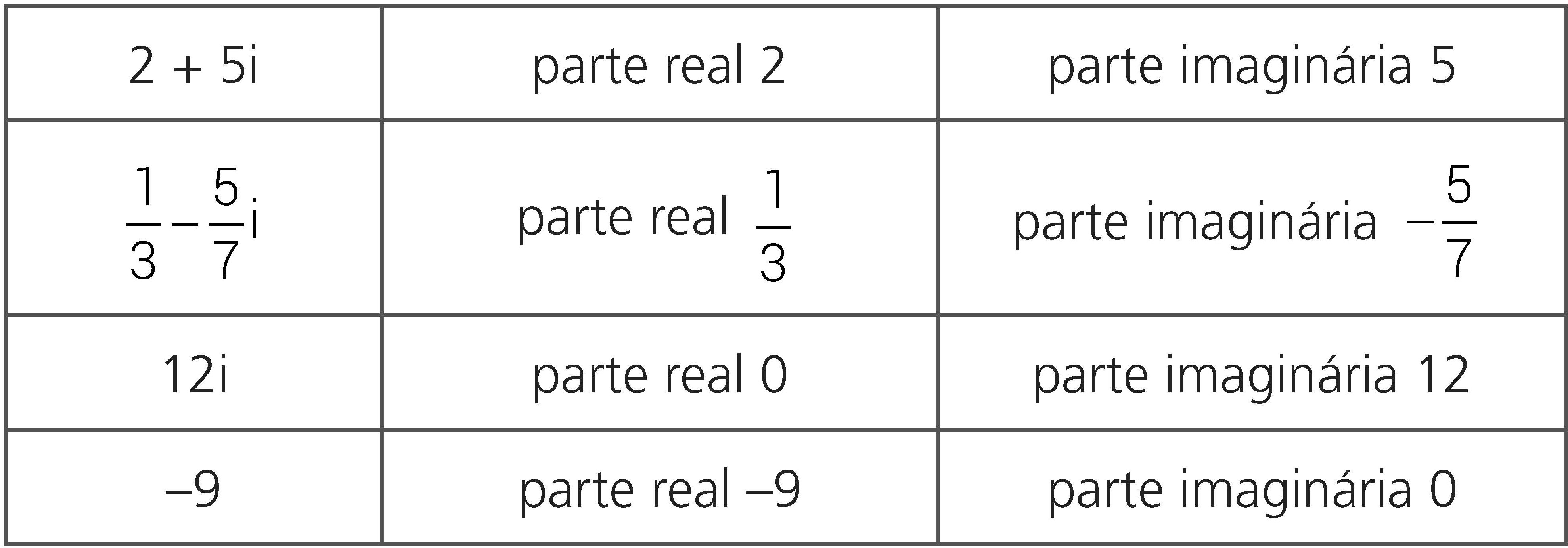
Um número como 12i, com parte real 0, chama-se número imaginário puro. Um número real como -9, pode ser considerado como um número complexo com parte imaginária 0.