DEFINIÇÃO DE MÓDULO
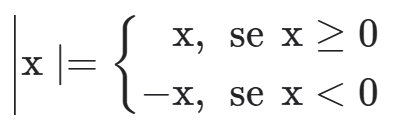
Exemplos: |1|=1,|-1|=1 e |0|=0.
PROPRIEDADES DO MÓDULO
a) |x|≥0
b) |-x|=|x|
c) -|x|≤x≤|x|
d) |x|·|y|=|x·y|∣
e) √x²=|x|
f) |x|²=x²
g) |x+y|≤|x|+|y| (desigualdade triangular)
h) |x|-|y|≤|x+y|
i) |x|-|y|≤|x-y|
FUNÇÃO MODULAR
É a função de ℝ em ℝ+ que associa a cada x o elemento seu módulo ou valor absoluto |x|.
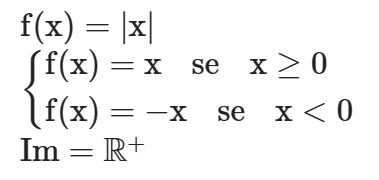
Na reta real, o módulo de x é a distância de x até a origem 0.
O gráfico da função modular é a união de duas semi-retas com origem na origem do plano cartesiano e que são bissetrizes do 1° e 2º quadrantes.
A imagem da função é Im=ℝ+, isto é, a função assume somente valores reais não negativos.
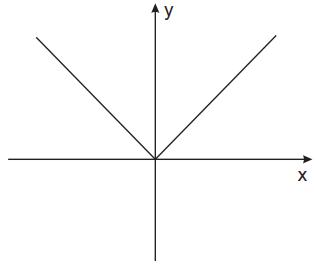
O gráfico das funções modulares compostas pode ser obtido traçando-se o gráfico da função original e espelhando-se a parte negativa em relação ao eixo x.
Gráfico de f(x)=|x+1|
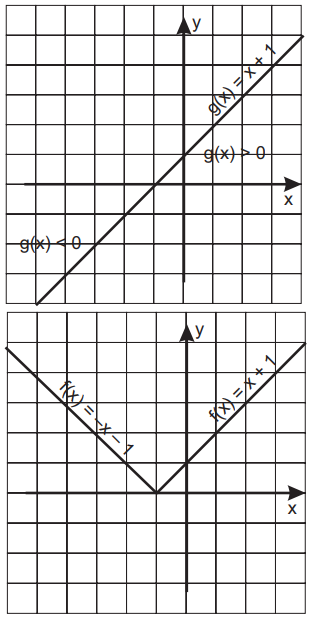
Outra maneira de traçar o gráfico de uma função modular composta é escrevendo-a sob a forma de uma função definida por várias sentenças abertas
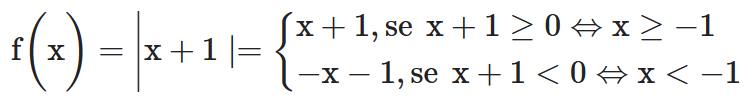
Ou seja, no intervalo (-∞,-1) o gráfico de f(x) é representado pelo gráfico de f1(x)=-x-1 e no intervalo [-1,+∞), pelo gráfico de f2(x)=x+1.




