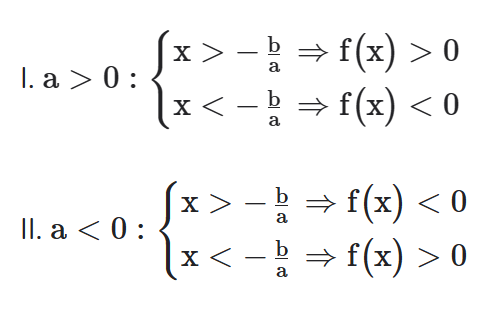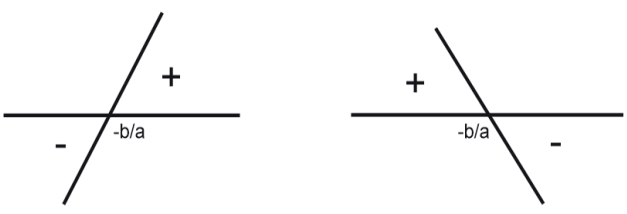DEFINIÇÃO
Uma função do 1º grau (ou função afim) é dada pela lei de formação f(x) = ax + b, com a, b ∈ ℝ e a ≠ 0. O número a é chamado de coeficiente angular de f e b é dito coeficiente linear.
Se a for igual a 0 , a função é chamada de função constante, exemplo y = 2.
O gráfico da função constante é sempre uma reta paralela ao eixo x, ou o próprio eixo x, no caso da reta y = 0.
ProBizu: o gráfico de qualquer função constante, com domínio R, é uma reta horizontal.
Observação: as raízes (ou zeros) de uma função f real são os valores que anulam tal função. Por exemplo, a raiz de é 5x + 3 é x = – 3/5. De forma mais geral, a ÚNICA raíz de f(x) = ax + b é x = – 3/5. Dizemos que uma função afim é linear se b=0, ou seja, uma função é linear se é da forma f(x) = ax, a ≠ 0.
GRÁFICO
Exemplo 1: gráfico da função do 1° grau, com domínio R dada por y = 2x -2.
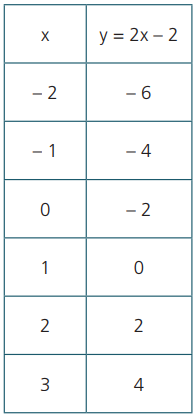
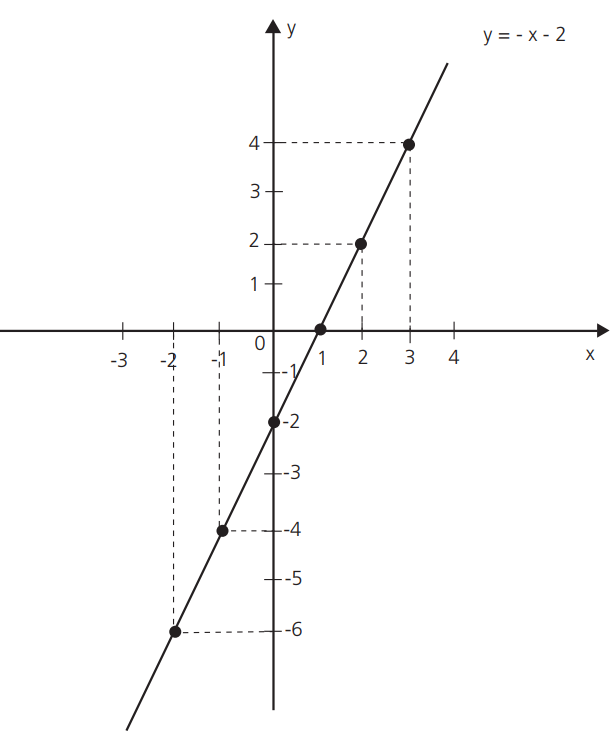
Observe que, nessa função, quanto maior é o valor de x, maior o valor de y.
Você pode ver isso na tabela, no gráfico ou na lei y = 2x – 2. (Aqui indica-se que x é adicionado. Assim, aumentando x, aumenta-se o valor que será adicionado. Portanto o valor de y diminuirá).
Essa função do 1° grau dada por y = – x – 2, é, portanto, decrescente.
Os exemplos que acabamos de ver são casos particulares de uma situação geral em que valem as seguintes afirmações:
Observação:
1º Chama-se função crescente aquela em que, aumentando o valor de x, sempre aumenta o valor de y.
2º Chama-se função decrescente aquela em que, aumentando o valor de x, sempre diminui o valor de y.
Exemplo 2: gráfico da função do 1° grau, com domínio R dada por y = – x – 2.
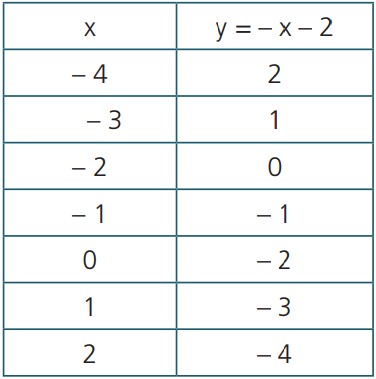
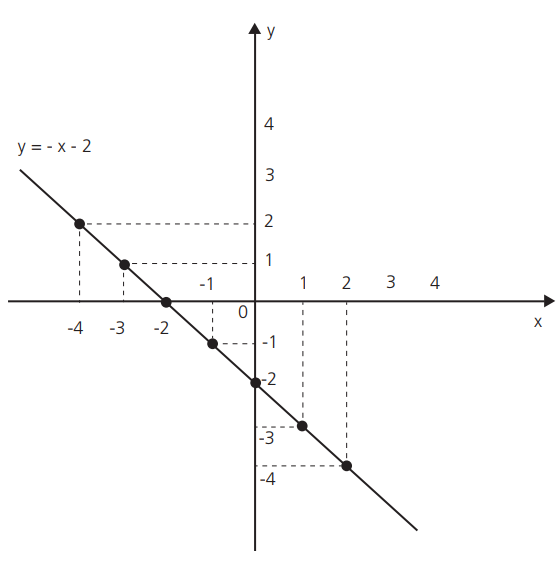
Observe que, nessa função, quanto maior é o valor de x, menor o valor de y. Você pode ver isso na tabela, no gráfico ou na lei y = – x.
Observação:
1º O gráfico de qualquer função do 1° grau com domínio R é uma reta.
2º Qualquer função do 1° grau dada por y = ax + b, com a > 0, é uma função crescente.
3º Qualquer função do 1° grau dada por y = ax + b, com a < 0, é uma função decrescente.
ProBizu: o gráfico de uma função afim é uma reta. Desta forma, para efetuar a construção de tal gráfico, basta que conheçamos dois de seus pontos. Em geral, escolhemos os pontos onde a reta corta o eixo x e o eixo y.
Observação: no gráfico, o coeficiente angular é igual à tangente do ângulo de inclinação da reta e o coeficiente linear é igual à ordenada do ponto de interseção da reta com o eixo das ordenadas (eixo y).
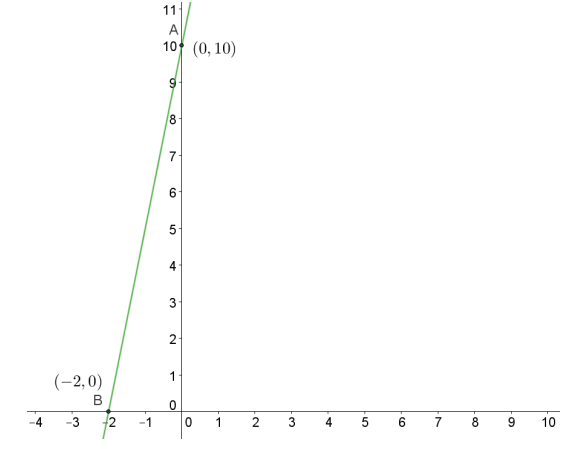
Vejamos agora um exemplo usando o nosso bizu: construir o gráfico de f(x) = 5x + 10.
A raiz desta função é x = –2. Assim, a nossa reta deve passar pelo ponto (–2, 0). Por outro lado, quando x = 0, a função assume valor igual a 10. Desta forma, a reta também deve passar pelo ponto (0,10). Estes dois pontos são suficientes para construirmos o gráfico:
COEFICIENTE ANGULAR E COEFICIENTE LINEAR
O coeficiente a é chamado coeficiente angular e representa a taxa de variação média da função Δy/Δx que é igual à tangente do ângulo de inclinação da reta. Sendo θ o ângulo de inclinação da reta, tem-se:

O coeficiente b é chamado coeficiente linear e é o ponto onde a reta cruza o eixo 0y, ou seja, a reta passa no ponto (0, b).
ESTUDO DO SINAL
Com isso, veremos agora como estudar o sinal de uma função afim, o que será extremamente útil na sequência do curso, quando estudarmos os quadros de sinais. Mais uma vez, o resultado é bastante simples e pode ser expresso através de um esquema. Temos o seguinte resultado.
TEOREMA: seja f(x) = ax + b, a ≠ 0, uma função afim. Então: