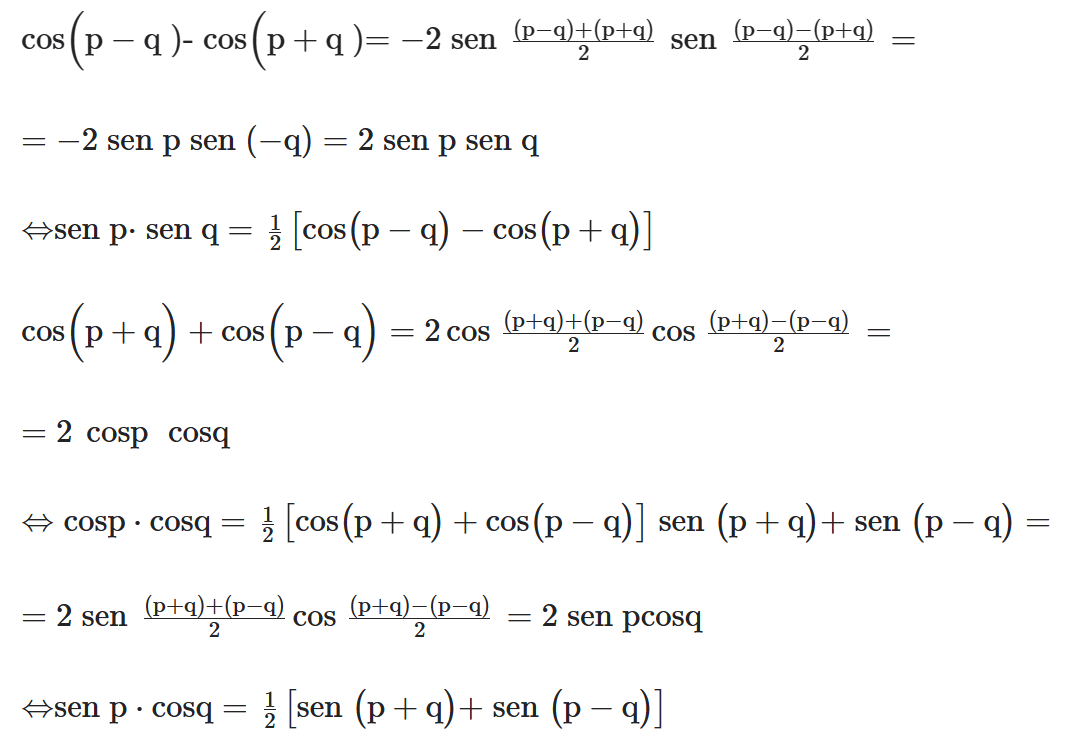FÓRMULAS DE ARCO SOMA E DIFERENÇA
As fórmulas a seguir permitem calcular o seno e o cosseno da soma e da diferença de arcos.

Demonstração:
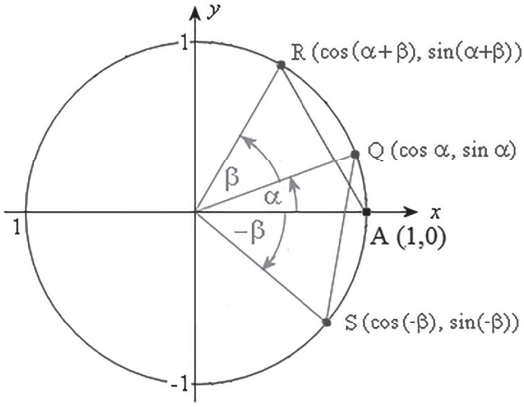
Sejam Q, R e S a imagem no ciclo trigonométrico de arcos com primeira determinação positiva α,(α + β) e (-β), respectivamente. Logo, AR⏜ = QS⏜, o que implica AR¯ = QS¯.
As coordenadas desses pontos são dadas por: Q = (cos α, sen α), R(cos(α + β), sen(α + β)) e S =(cos(-β), sen(-β)) = (cosβ,-senβ).
Aplicando a fórmula de distância entre pontos, temos:
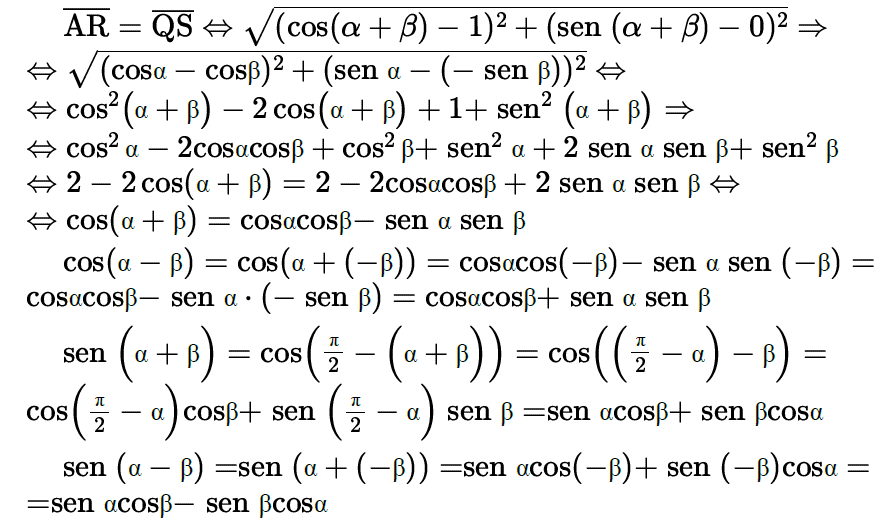
As fórmulas a seguir permitem o cálculo da tangente da soma e da diferença de arcos, com α, β, α + β, α – β ≠ π/2 + kπ, k ∈ ℤ.
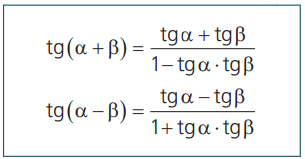
Demonstração:

Exemplo: calcule o seno, o cosseno e a tangente de 15°.
Resolução:
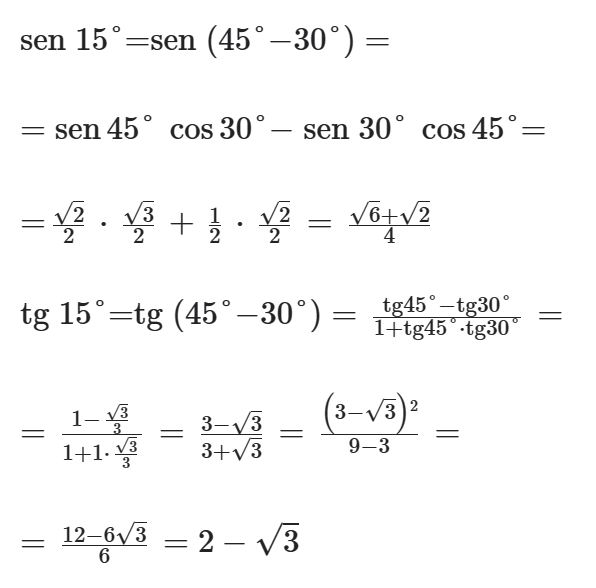
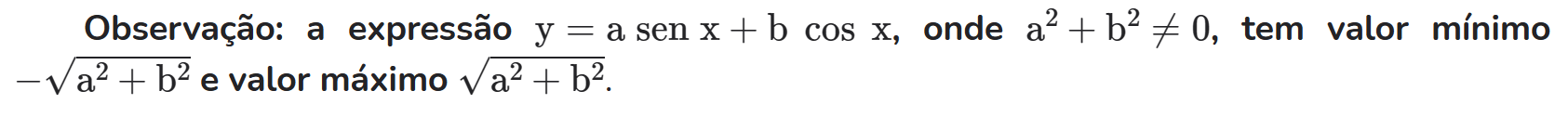
Demonstração
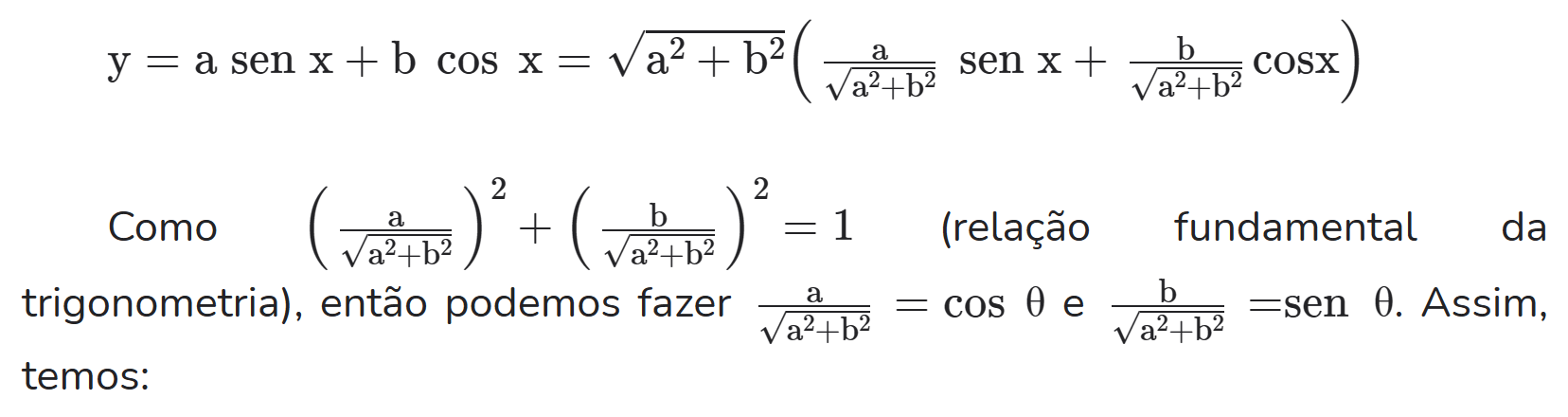
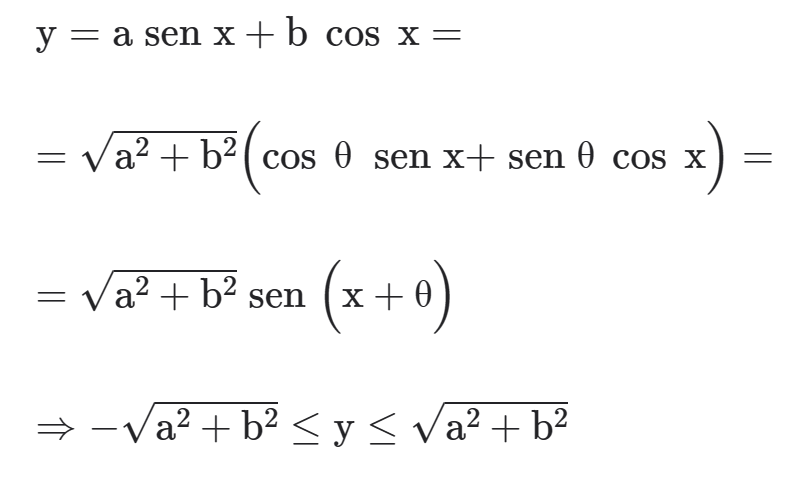
FÓRMULAS DE ARCO DOBRO E TRIPLO
As fórmulas a seguir permitem calcular o seno, o cosseno e a tangente do dobro de um arco.

Demonstração:
sen 2 α = sen(α + α)=
=sen α cos α + sen α cos α =2 sen α cos α cos 2 α = cos(α + α) = cos α cos α – sen α sen α=
=cos2 α – sen2 α = cos2 α = cos2 α – sen2 α=
=cos2α – (1 – cos2 α) = 2 cos2α – 1 = cos 2α =
=cos2α – sen2α = (1 – sen2α) – sen2α = 1 – 2 sen2 α
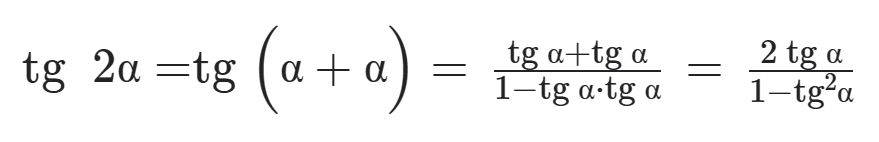
Note que a fórmula de tg 2 α só é válida se 2 α ≠ π/2 + kπ, k ∈ ℤ.
As fórmulas a seguir permitem calcular o seno, o cosseno e a tangente do triplo de um arco.
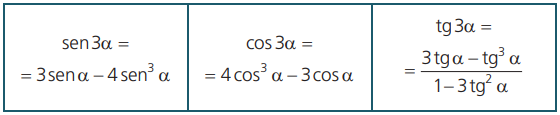
Demonstração:
Demonstração:
sen 3α = sen (2α + α) = sen 2α cos α + sen α cos 2α =
=2sen α cos α · cos α + senα · (1 – 2sen2 α)=
=2sen α(1 – sen2 α) + sen α – 2sen3 α=
= 3sen α – 4 sen3 α
cos 3α = cos(2α + α) = cos 2α cos α – sen 2α sen α=
=(2cos2α – 1) · cos α – 2sen α cos α · sen α=
=2cos3 α – cos α – 2cos α(1 – cos2α)=
=4cos3 α – 3cos α
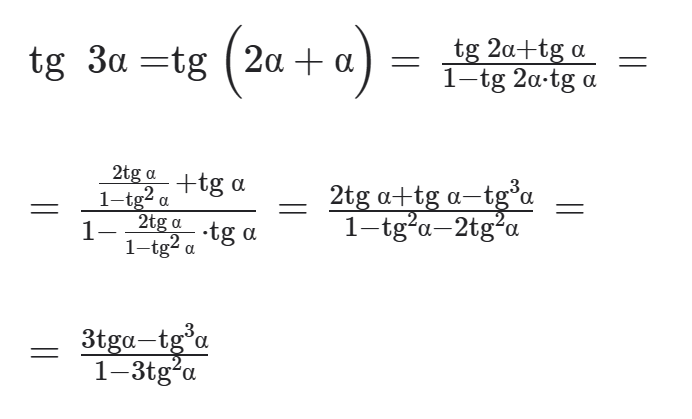
FÓRMULAS DE ARCO METADE
As seguintes fórmulas permitem calcular o seno, o cosseno e a tangente da metade de um arco, a menos do sinal.
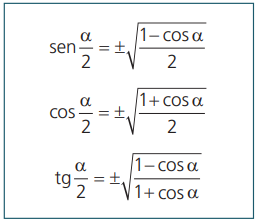
Demonstração:
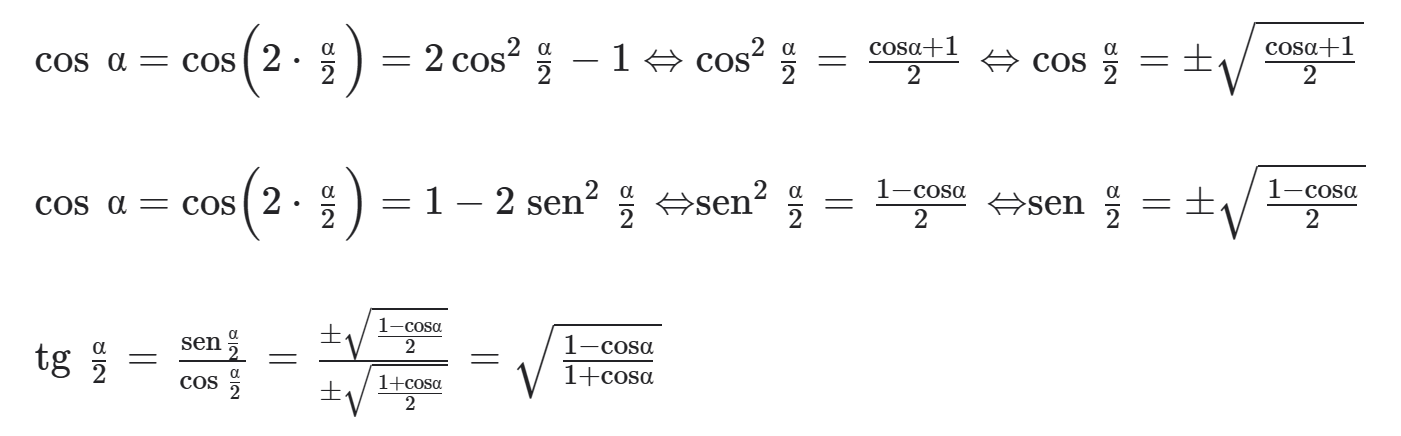
Exemplo: calcule o seno, o cosseno e a tangente de π/8.
Resolução: como π/8 ∈ QI, então todas as suas linhas trigonométricas são positivas.
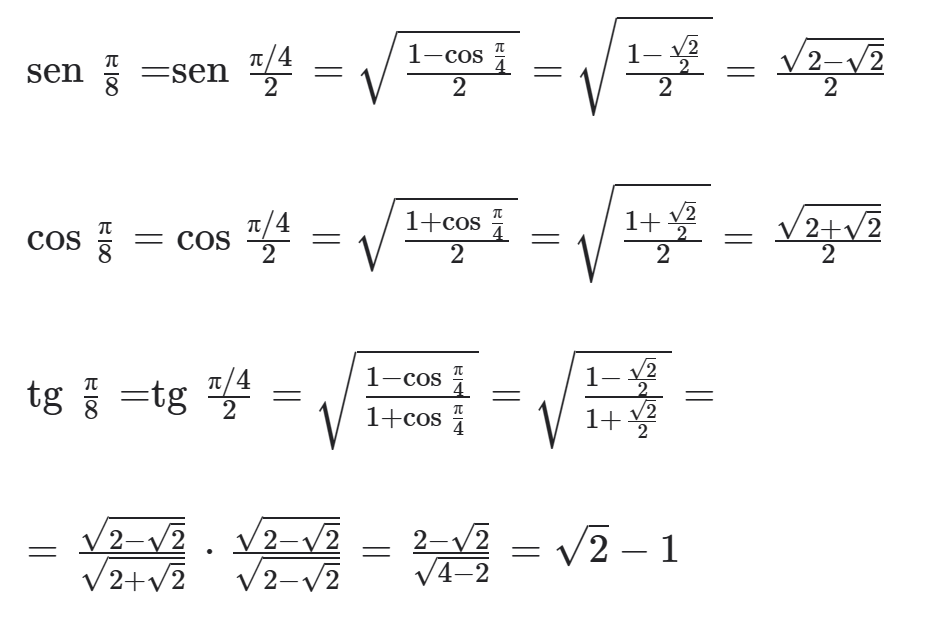
FÓRMULAS DE DUPLICAÇÃO USANDO TANGENTE
As seguintes fórmulas permitem calcular o seno e o cosseno de um arco conhecendo-se a tangente do seu arco metade.

Demonstração:
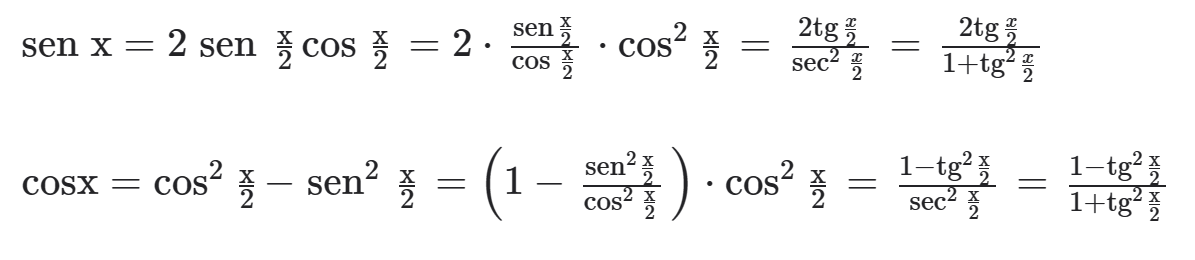
A fórmula seguinte permite calcular a tangente da metade de um ângulo conhecendo-se o seno e o cosseno do ângulo.
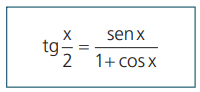
Demonstração:
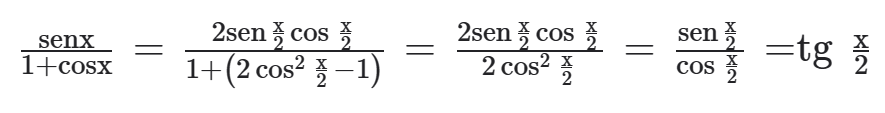
Essa relação pode ser facilmente identificada no ciclo trigonométrico para ângulos agudos. Basta fazer AÔP = x, o que implica AÂ’P = x/2 (ângulo inscrito) e podemos calcular a tg x/2 dividindo o cateto oposto sen x pelo cateto adjacente 1 + cos x.
FÓRMULAS DE PROSTAFÉRESE OU DE WERNER
As fórmulas de Prostaférese ou de Werner permitem transformar somas ou diferenças de senos, cossenos e tangentes em produtos ou vice-versa.
As fórmulas a seguir permitem transformar somas e diferenças em produtos.

Demonstração:
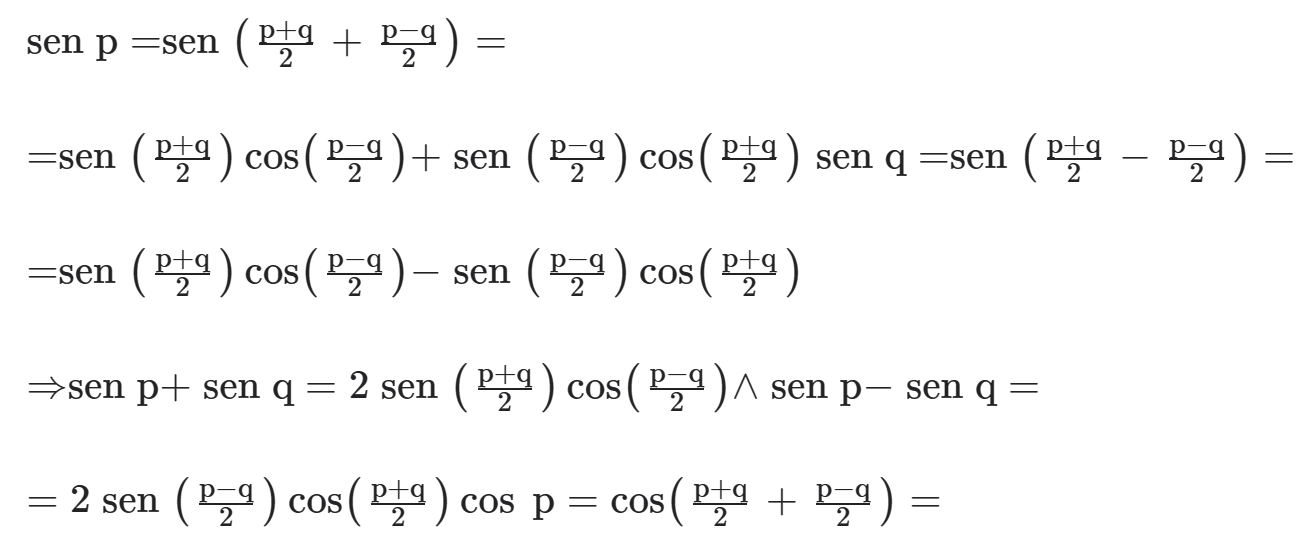

As fórmulas a seguir permitem transformar produtos em soma.

Demonstração: