A fração é representada por uma das seguintes formas:
A/B ou A/B , com A, B∈N e B≠0
Onde:
A é chamado de numerador e indica quantas partes a fração tem.
B é chamado de denominador e indica em quantas partes a unidade foi dividida.
Exemplos:
a) A fração 3/5 indica que a unidade foi dividida em 5 partes e nós temos 3 delas. Nesse exemplo o numerador é 3 e o denominador é 5.
b) Podemos representar as frações por meio de figuras. Por exemplo: Júlia comeu 3/8 de um chocolate. Isso quer dizer que se o chocolate for dividido em 8 partes iguais, Júlia comeu 3 dessas partes. Veja a figura que representa essa fração:

Na figura acima, as partes amarelas representam aquelas que Júlia comeu (3/8) e a parte branca é a que sobrou (5/8) do chocolate.
Leitura de frações
As frações recebem nomes especiais de acordo com os numeradores e denominadores usados. Quando o denominador for maior que 10 acrescentamos a palavra “avos” ao denominador.
Veja alguns exemplos:
1/2 : um meio; 2/3 : dois terços; 3/4 : três quartos; 3/5 : três quintos; 5/7 : cincos sétimos; 6/10 : seis décimos; 7/18 : sete dezoito avos; 11/15 : onze quinze avos; 7/30 : sete trinta avos; 60/100 : sessenta centésimos; 8/1000 : oito milésimos; 3/2 : três meios; 16/9 : dezesseis nonos.
Observação: quando o denominador é múltiplo de 10 podemos acrescentar avos ao denominador ou usar o substantivo ordinal correspondente ao denominador.
Exemplo:
1/20: podemos ler essa fração como um vinte avos ou um vigésimo.
Classificação das frações
Temos três tipos de frações:
Frações próprias:
São aquelas cujo numerador é menor que o denominador e elas representam números menores que um inteiro.
Exemplos : 1/3 , 7/9 , 23/72
Usando uma representação simbólica:
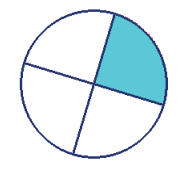
Representa a fração própria 1/4
Observação As fraçõ es cujos denominadores são potência de 10 (10, 100, 1000, …) são chamadas de frações decimais.
Exemplos: 3/10 , 23/100 , 435/1000
Frações impróprias
São aquelas cujo numerador é maior que o denominador e elas representam números maiores que um inteiro.
Exemplos: 5/2 , 11/6 , 23/7
A figura abaixo representa a fração imprópria 8/6.
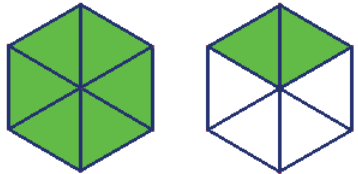
Observação: as frações impróprias podem ser constituídas de uma parte inteira e uma parte fracionária. Quando são escritas dessa maneira recebem o nome de frações mistas.
Exemplos: 1 2/6 , 3 1/4
Frações aparentes
São as frações cujo numerador é múltiplo do denominador. Se dividirmos os numeradores dessas frações pelos seus respectivos denominadores iremos obter valores inteiros.
Exemplos: 9/3 , 28/7 , 6/6, que, na verdade, representam, respectivamente, os números: 3,4 e 1.
Usando a representação em figura:
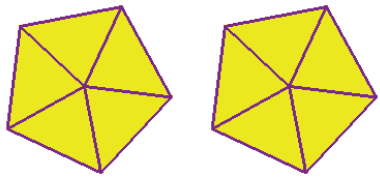
Representa a fração aparente 10/5 que é igual a 2, ou seja, 2 unidades.
Exemplos:
a) 3 1/4
b) 5 1/7
Podemos representar uma fração mista através de figuras. Por exemplo, vamos representar a fração do item (a). Como o denominador é 4, concluímos que a unidade é dividida em 4 partes e pela fração vemos que temos três unidades mais um quarto da unidade. A fração, representada pela parte colorida, será:
Equivalência de frações
Frações equivalentes são aquelas que representam a mesma parte do todo. Quando comparamos uma com a outra, verificamos que tanto o numerador como o denominador é multiplicado pelo mesmo número.
Exemplo:
As frações 2/3 , 6/9 , 30/45 são equivalentes.
A segunda fração acima é obtida multiplicando-se o numerador e o denominador da primeira fração por 3 e a terceira fração acima é obtida multiplicando-se o numerador e o denominador da primeira fração por 15.
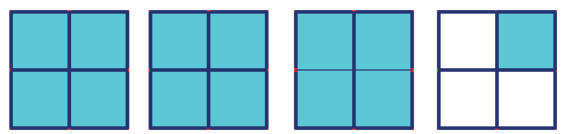
Podemos representar por meio de figuras, frações equivalentes.
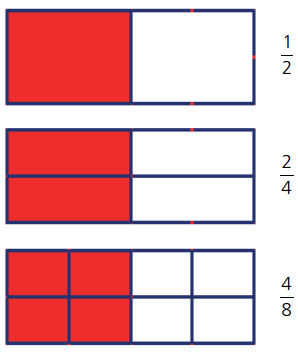
Na figura acima, as três frações são equivalentes. Observe que qualquer uma delas representa a metade do todo (esse é o retângulo maior).
As duas últimas frações da figura foram obtidas da seguinte forma: 1×2/2×2 =2/4 e 1×4/2×4 = 2/8.
Então podemos deduzir que: para determinarmos frações equivalentes a uma fração dada devemos multiplicar o numerador e o denominador por um mesmo número natural, diferente de zero.
Simplificação de frações
Para simplificar uma fração devemos dividir, simultaneamente, o numerador e o denominador por um fator comum. Esse fator comum, na verdade, é o M.D.C. do numerador e denominador.
Exemplos:
Simplificar as frações:
a) 3/15
O M.D.C. (15,3)=3, então dividimos o numerador e o denominador por 3, obtendo-se: 3×1/3×5=1/5.
b) 14/49
O M.D.C. (49,14)=7, então dividimos o numerador e o denominador por 7, obtendo-se: 7×2/7×7=2/7.
c) 11/17
O M.D.C. (17,11)=1, quando isso acontece dizemos então que a fração é irredutível.
Nos itens (a) e (b) acima as frações resultantes da simplificação efetuada, 1/5 e 2/7, também são irredutíveis, pois M.D.C. (5,1)=1 e M.D.C. (7,2)=1.
Podemos então definir: fração irredutível é aquela que o numerador e o denominador não têm nenhum fator em comum, ou seja, M.D.C. (denominador, numerador) = 1.




