M.M.C E M.D.C. DE POLINÔMIOS
O máximo divisor comum (M.D.C.) entre polinômios é o polinômio unitário formado pelos fatores comuns aos polinômios elevados aos seus menores expoentes, de forma que ele é o polinômio de maior grau que divide todos aqueles.
As raízes comuns aos polinômios são também raízes de seu MDC, com a menor multiplicidade.
Se o MDC de dois polinômios é 1, diz-se que eles são primos entre si.
Quando os polinômios não estão na forma fatorada, o seu MDC pode ser obtido pelo método das divisões sucessivas.
Exemplo:
Obtenha o MDC dos polinômios p(x) = x4 – 3x³ + 3x² – 3x + 2 e q(x) = x² – 4x + 3.
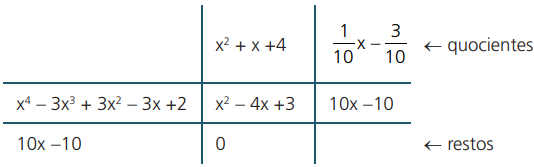

vale notar que a divisão por 10 se faz necessária para que o mdc seja um polinômio unitário.
O mínimo múltiplo comum entre polinômios é o polinômio unitário formado por todos os fatores que aparecem nos polinômios, comuns ou não, elevados ao seu maior expoente, de forma que ele é o polinômio de menor grau que é múltiplo de todos aqueles. Todas as raízes dos polinômios são raízes do seu mmc.
Exemplos:
P(x) = x(x – 1)²(x – 2)³ e Q(x) = x³(x-1)(x-3)²
mdc(P,Q) = x(x – 1)
mmc(P,Q) = x3(x – 1)²(x – 2)³(x – 3)²
EQUAÇÕES ALGÉBRICAS
Sendo P(x) um polinômio em C, chama-se equação algébrica à igualdade P(x)=0. Portanto, as raízes da equação algébrica, são as mesmas do polinômio P(x). O grau do polinômio, será também o grau da equação.
Exemplo:
3x4 – 2x3 + x + 1 = 0 é uma equação do 4º grau.




