LENTES
As lentes são os instrumentos que utilizam a refração para produzir imagens. Elas serão classificadas de acordo com a trajetória dos raios luminosos que incidem nelas. Para construir uma lente, devemos juntar dois dioptro transparentes com pelo menos um deles curvo. Faremos uso apenas de dioptros esféricos, que podem ser côncavos ou convexos.
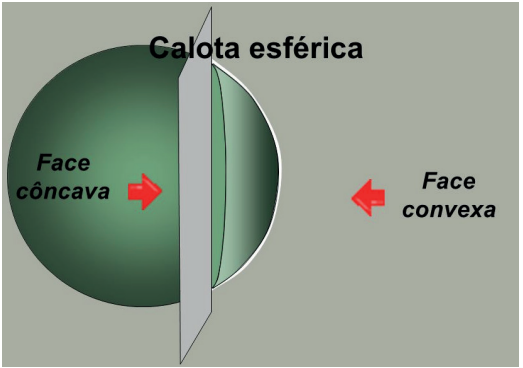
Tipos de superfícies esféricas
CLASSIFICAC̣ÃO DAS LENTES
De posse dessas calotas esféricas e do dioptro plano, podemos montar seis diferentes tipos de lentes, que serão classificadas de duas formas de acordo com o formato das suas pontas: finas ou grossas.
BORDAS FINAS

BORDAS GROSSAS

De acordo com o comportamento de um feixe de raios paralelos incidindo sobre a lente, podemos classicá-las de outras duas maneiras:
CONVERGENTES
Nessas lentes, o feixe de raios paralelos converge para um ponto
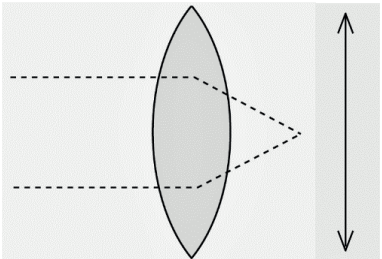
Representação de uma lente convergente
DIVERGENTES
Nessas lentes, o feixe de raios paralelos diverge de um ponto
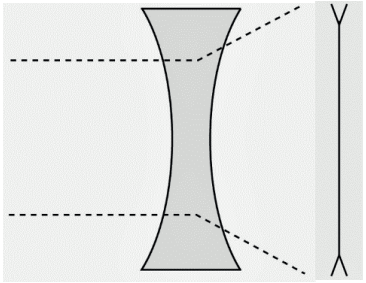
Representação de uma lente divergente
LENTES DELGADAS
Ao fabricarmos as lentes, a distância entre as suas superfícies é muito pequena, se comparada à curvatura das esferas que a deram origem, ou seja, a espessura é desprezível. Chamamos essas lentes de delgadas e serão o objeto principal do nosso estudo.
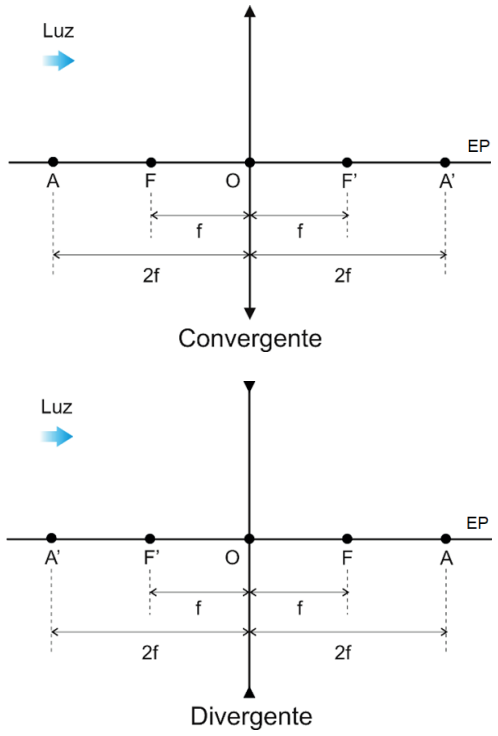
Na figura acima, representamos os principais pontos de uma lente:
- EP: eixo principal
- FO¯=F’O¯= f: distância focal
- Centro óptico (O): é o ponto do eixo principal por onde passa um raio luminoso que não sofre desvio angular.
- Foco imagem (F’): ponto de convergência dos raios incidentes paralelos ao eixo principal
- Foco objeto (F): pelo princípio da reversibilidade, os raios que incidem passando pelo foco, saem paralelos ao eixo principal
- Ponto antiprincipal objeto (A): ponto cuja distância do centro óptico é o dobro da da distância do foco objeto.
- Ponto antiprincipal imagem (A’): ponto cuja distância do centro óptico é o dobro da da distância do foco imagem.
Observação O foco objeto de uma lente convergente é real, enquanto de uma lente divergente é virtual.
RAIOS LUMINOSOS PARTICULARES
A fim de determinarmos as características das imagens formadas pelas lentes, precisamos conhecer a trajetória dos raios luminosos que as atravessam. Existem três raios cujas trajetórias nos serão imediatas.
- Raio incidente ao eixo principal sofre refração passando pelo foco imagem.
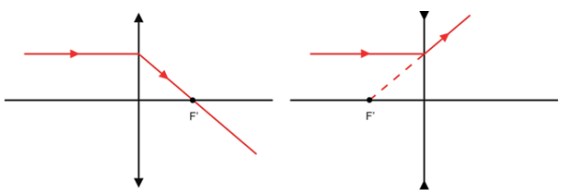
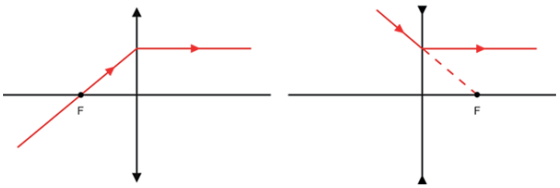
- Raio incidente passando pelo foco objeto sofre refração paralelamente ao eixo principal.
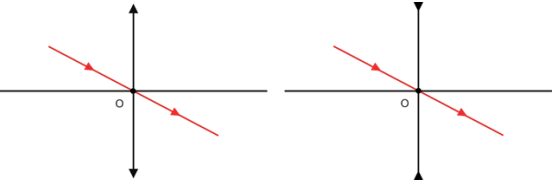
- Raio incidente passando pelo centro óptico sofre refração sem sofrer desvio.
CONSTRUÇÃO DE IMAGENS
Para construirmos graficamente as imagens, vamos fazer uso desses raios particulares para diversas posições do objeto na frente de cada tipo de lente.
LENTES CONVERGENTES
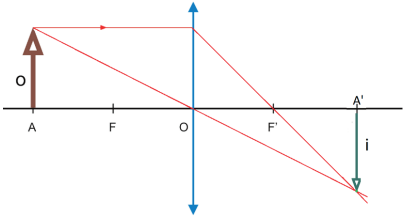
- Objeto real antes do ponto antiprincipal objeto
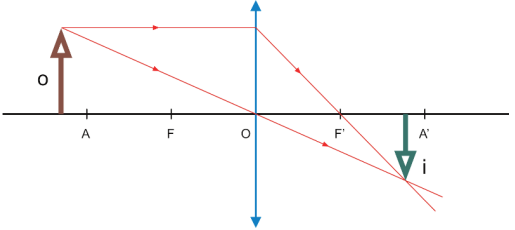
A imagem é real, invertida e menor.
Aplicação: usada nas antigas máquinas fotográficas
- Objeto real sobre o ponto antiprincipal objeto
A imagem é real, invertida e de mesmo tamanho.
Aplicação: usada nas máquinas fotocopiadoras (xerox)
Objeto real entre o ponto antiprincipal objeto e o foco objeto
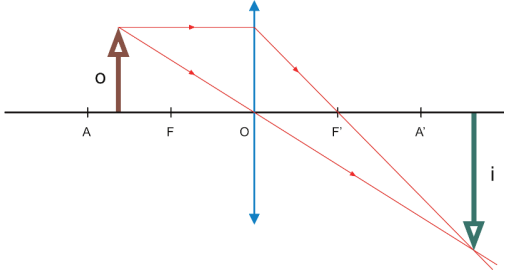
A imagem é real, invertida e maior.
Aplicação: usada nos antigos projetores de slides.
- Objeto real sobre o foco objeto
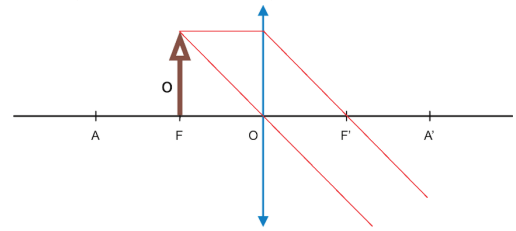
A imagem é imprópria
- Objeto real entre o foco objeto e o centro óptico
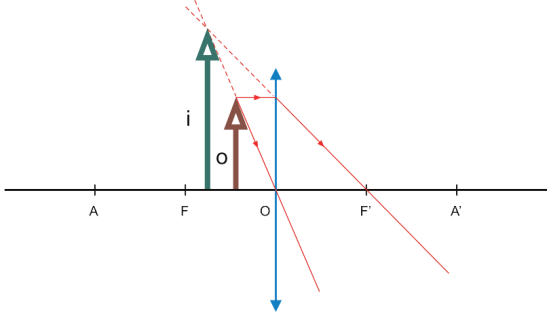
A imagem é virtual, direita e maior.
Aplicação: usada nas lupas para ampliar a imagem
LENTES DIVERGENTES
- Objeto real em uma posição qualquer
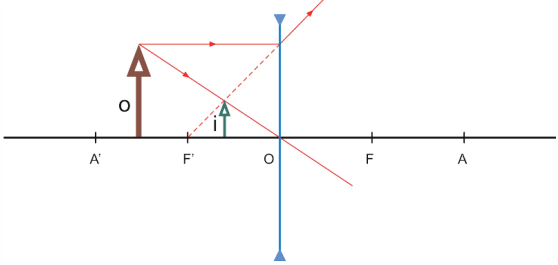
A imagem é virtual, direita e menor.
Aplicação: usada nos óculos de pessoas míopes.
EQUAÇĀO DE GAUSS
Já sabemos construir graficamente a imagem e identificar a sua localização em relação aos pontos da lente. Agora vamos determinar a posição e o tamanho das imagens geradas pelas lentes a partir de uma equação de Gauss idêntica àquela utilizada em espelhos curvos.

em que:
- Lente s convergentes: f>0
- Lentes divergentes: f<0
- Objetos reais: p>0
- Objetos virtuais: p<0
- Imagens reais (“imagem do lado oposto ao do objeto”): p’>0
- Imagens virtuais (“imagem do mesmo lado que o objeto”): p’<0
Para o cálculo do tamanho da imagem, usamos a equação da ampliação linear:

Em que:
- i é o tamanho da imagem
- o é o tamanho do objeto
- A é ampliação gerada pela lente
Observação:
- Se a ampliação for negativa, a imagem é invertida em relação ao objeto
- Se a ampliação for positiva, a imagem é direita em relação ao objeto
EQUAÇÃO DE HALLEY
As lentes foram classificadas quanto à sua borda e quanto à trajetória dos raios luminosos. Vamos agora associar o comportamento de cada tipo de lente.
VERGÊNCIA
Nem todas as lentes de um mesmo tipo são iguais. Cada uma tem um poder em alterar a trajetória da luz que passa por ela. Essa grandeza é chamada de vergência e é definida como o inverso da distância focal.

- Se V>0, a lente é convergente
- Se V<0, a lente é divergente
Observação:
- A unidade SI da vergência é m-1 ou dioptria (di).
- Na linguagem popular, constuma-se chamar a vergência de “grau”.
EQUAÇÃO DO FABRICANTE DE LENTES
Essa equação será capaz de relacionar o material da lente, o meio onde ela está imersa e a curvatura dos dioptros para determinar a sua distância focal ou a sua vergência:
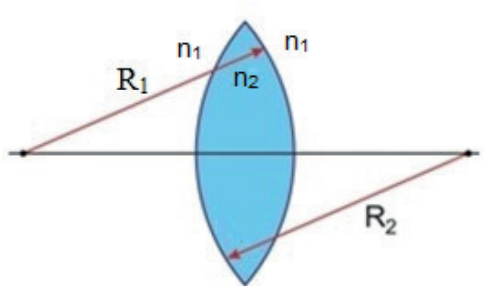

- n2 é índice de refração do material que compõe a lente
- n1 é índice de refração do meio em que a lente está imersa
- R1 e R2 são os raios de curvatura das superfícies da lente.
- Superfície côncava: R >0
- Superfície convexa: R < 0
Para você não ficar usando todas as vezes a fórmula para determinar o tipo de lente, a tabela abaixo mostra o sinal das vergências de cada tipo de lente de acordo a relação entre os índices de refração:
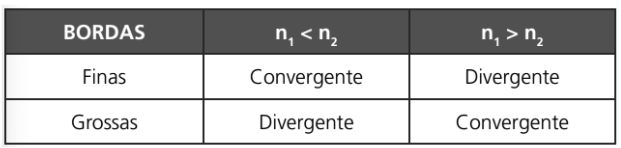
ATENÇÃO! Como normalmente as lentes estão imersas no ar, costumamos dizer que as lentes de bordas finas são convergentes e as de bordas grossas são divergentes.
INSTRUMENTOS ÓPTICOS
De posse de algumas lentes específicas, podemos construir instrumentos ópticos que nos auxiliam na visualização de objetos, desde pequenas partículas próximas até estrelas e planetas longínquos.
LUPA
A lupa ou microscópio simples é formada por uma única lente convergente e o objeto é posto entre o foco o centro óptico a fim de criar imagens ampliadas e direitas, sendo, portanto, virtuais.
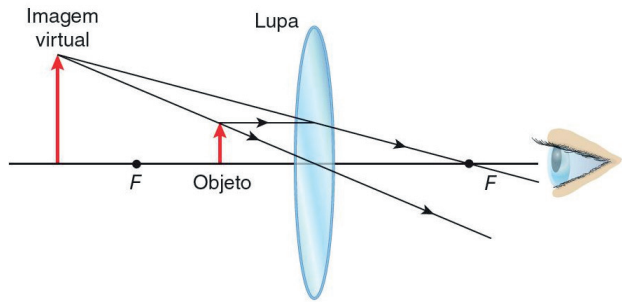
Formação de imagem em uma lupa
MICROSCÓPIO COMPOSTO
O microscópio composto é formado por duas lentes convergentes causando um aumento ainda maior que com apenas uma. A primeira lente é a objetiva, com alta vergência (pequena distância focal). A segunda lente também é convergente e chamada de ocular e permite ao observador ver uma imagem final virtual, direita e maior que o objeto.
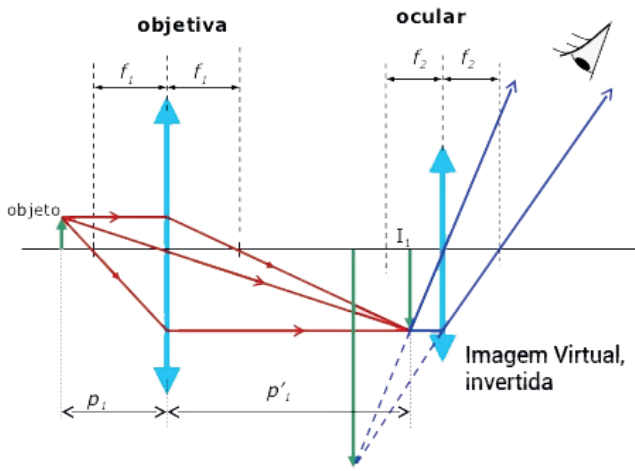
Formação das imagens em um microscópio composto
A imagem final da associação das duas lentes é virtual, invertida e ampliada. Essa ampliação pode ser determinada pela seguinte equação:

LUNETA ASTRONÔMICA
As lunetas astronômicas possuem duas lentes convergentes e são usadas na observação de objetos muitos distantes
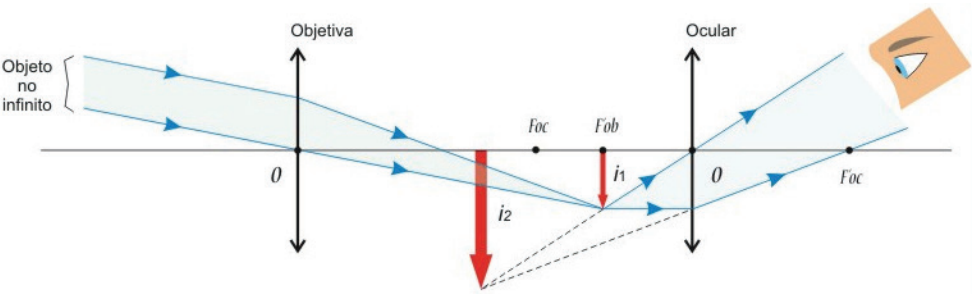
Formação das imagens em uma luneta astronômica
LUNETA TERRESTRE
A luneta terrestre possui uma lente objetiva covergente e uma lente ocular divergente.
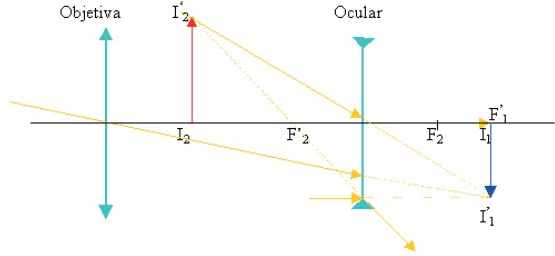
Formação das imagens em uma luneta terrestre
Observação: para as lunetas não há aumento linear, no entanto há um aumento no ângulo de visada do observador dando a percepção de que o objeto aumentou. Essa ampliação angular é calculada pela expressão abaixo:

OLHO HUMANO
O olho também pode ser visto como um instrumento óptico, tendo o cristalino como uma lente biconvexa e convergente. Os raios produzem imagem na retina onde as informações são levadas pelo nervo óptico ao cérebro. Como estamos interssados apenas no comportamento óptico, podemos representar o olho como na figura abaixo:
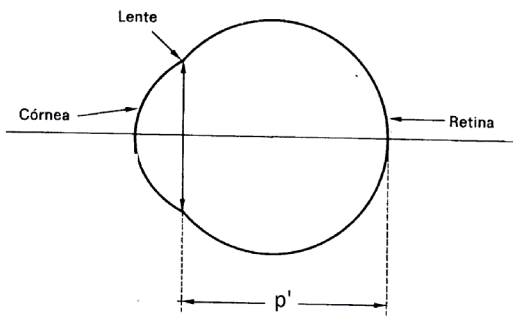
Representação simplificada do olho
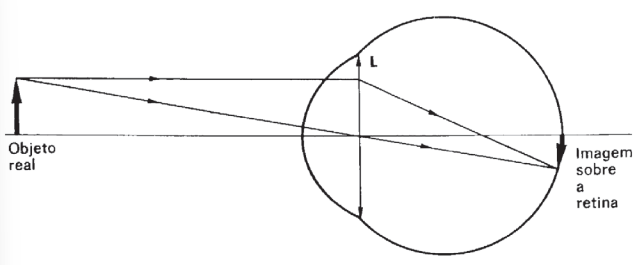
Representação da imagem gerada pelo olho
COMODAÇÃO VISUAL
Para manter a imagem em foco (sobre a retina) para diversos objetos, nossos olhos contraem ou relaxam para mudar a sua curvatura e, consequentemente, a sua vergência (vide equação de Halley). Vamos destacar dois pontos principais dessa acomodação e suas características.
PONTO REMOTO (PR)
- Objeto muito longe (no infinito)
- O foco-imagem da lente coincide com a retina
- Ausência de tensão nos músculos ciliares
- Distância focal máxima
- Vergência mínima
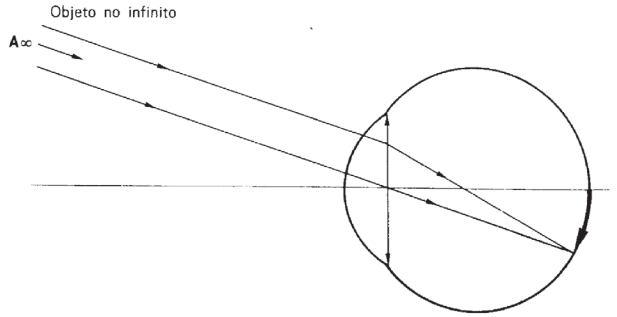
Representação da imagem do ponto remoto
PONTO PRÓXIMO (PP)
- Objeto a cerca de 25 cm do olho
- Distância mínima de visão distinta: ponto mais próximo dos olhos que conseguimos enxergar sem forçar a vista além do necessário
- Tensão máxima nos músculos ciliares
- Distância focal mínima
- Vergência máxima
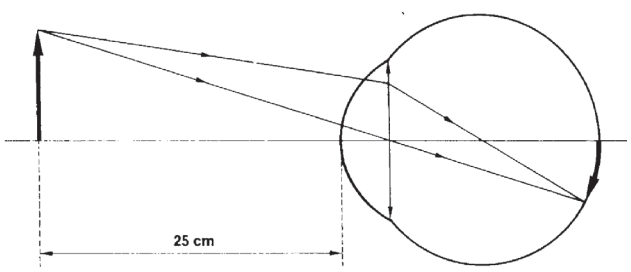
Representação da imagem do ponto próximo
DEFEITOS DA VISÃO
Se, por exemplo, quando olhamos pro céu noturno e não distingumos a luz das estrelas da iluminação pública ou precisamos afastar muito um livro para sermos capazes de ler, temos um problema de visão que pode ser corrigido usando os óculos. Vamos falar apenas dos casos que podem corrigidos pelas lentes.
MIOPIA
- Problema para enxergar de LONGE
- O cristalino possui ALTA convergência
- A imagem se forma antes da retina
- Correção: lentes DIVERGENTES
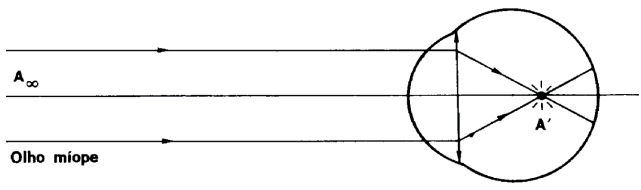
Olho míope enxergando o ponto remoto
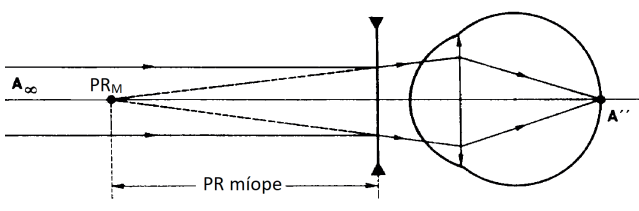
Olho míope corrigido com uma lente divergente
HIPERMETROPIA
- Problema para enxergar de PERTO
- O cristalino possui BAIXA convergência
- A imagem se forma depois da retina.
- Correção: lentes CONVERGENTES.
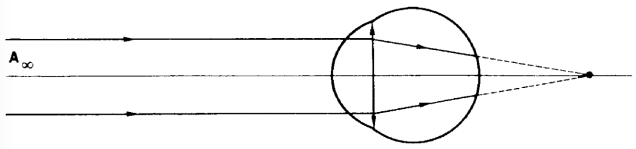
Olho hipermétrope enxergando o ponto remoto
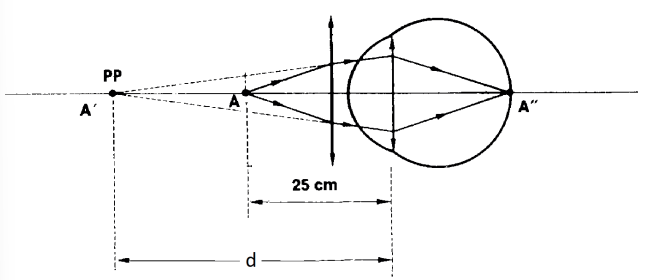
Olho hipermétrope corrigido enxergando o ponto próximo
PRESBIOPIA
- Também conhecida como VISTA CANSADA
- Defeito nos músculos ciliares
- Correção: lentes CONVERGENTES.
ASTIGMATISMO
- Defeito no formato da CÓRNEA
- A imagem se forma sobre a retina, mas sem nitidez
- Correção: lentes CILÍNDRICAS.
ESTRABISMO
- Desalinhamento dos olhos
- Não há, em geral, nenhum problema na visão
- Correção: lentes PRISMÁTICAS.




