PRIMEIRA LEI DE NEWTON
Todo corpo em repouso ou em movimento retilíneo uniforme continua nesses estados, a menos que seja obrigado a alterá-los por forças aplicadas sobre ele.
Se nenhuma força atuar sobre um corpo ele deverá permanecer em repouso. Para que um corpo deixe de estar em repouso deverá sobre ele ser aplicada uma força, mas se, após o início do movimento, essa força deixar de atuar sobre o corpo, este corpo deverá permanecer em movimento retilíneo uniforme.
Podemos entender a inércia de um corpo como a propriedade que esse corpo tem de resistir à mudança de velocidade.
A primeira Lei de Newton é também chamada de Lei da Inércia ou Princípio da Inércia.
Imagine você dentro de um ônibus, com certeza você já percebeu que quando o ônibus, que está em movimento, começa a frear, você sente seu corpo tendendo a ser “arremessado” no sentido de movimento do ônibus. Isso se dá pela inércia, seu corpo tende a continuar em movimento, por isso é sempre bom se segurar!
Assim se a força resultante sobre um corpo for nula este corpo estará em repouso em movimento retilíneo uniforme.
Referencial inercial
O referencial será dito inercial se estiver em repouso ou em movimento retilíneo uniforme. As leis de Newton são válidas somente para referenciais inerciais.
O movimento de rotação da Terra faz com que nosso planeta não seja considerado um referencial inercial, pois estando em movimento circular haverá a atuação da força centrípeta; se há força haverá aceleração. Para movimentos de pequena duração, o efeito da rotação da Terra pode ser desconsiderado, nesses casos o planeta será considerado um referencial inercial.
SEGUNDA LEI DE NEWTON
Sendo F→ a resultante das forças que atuam sobre um corpo de massa m temo que F→ = m · a→, onde a→ é a aceleração do corpo.
Sendo a massa uma grandeza escalar e sempre positiva temos que F→ e a→ possuirão sempre mesma direção e mesmo sentido.
Unidades de força
No SI a unidade de força é o newton, cujo símbolo é N. Assim, considerando a equação F→ = m · a→, temos:

Movimentos acelerado e retardado
A força F→ tem o mesmo sentido da velocidade v→
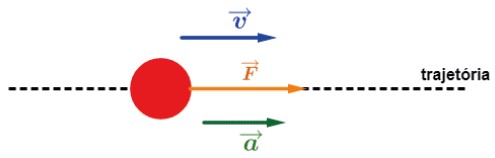
Nesse caso, a aceleração a→ também tem o mesmo sentido de v→ e o movimento é acelerado, isto é, o módulo de v→ aumenta com o tempo.
A força F→ e a velocidade v→ têm sentidos opostos
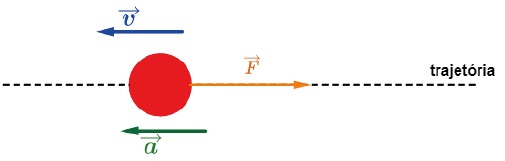
Como a aceleração a→ deve ter o mesmo sentido de F→, o sentido de é oposto ao sentido de a→ e o movimento é retardado, isto é, o módulo de v→ diminui com o tempo.
Exercício Resolvido 1: Um ponto material de massa m = 600 g está em movimento retilíneo acelerado, cuja aceleração tem módulo a = 5,0 m/s². Calcule o módulo da resultante das forças que atuam no ponto material.
Resolução:
No SI, a unidade de massa é o quilograma (kg). Assim: m = 600 g = 0,6 kg
Sendo F→ a resultante das forças que atuam no ponto material, temos pela Segunda Lei de Newton: F→ = m · a→. Portanto: F = (0,6) · (5,0) = 3,0 N
Força peso e força normal
A Terra exerce uma força de atração sobre todos os corpos situados em sua proximidade. Essa força será chamada de força peso e será representada por P→. A força peso sempre terá a direção da reta que passa pelo centro da Terra e o sentido será do corpo para o centro da Terra. Nas análises de movimentos que faremos sempre iremos considerar as distâncias dos corpos em relação a superfície como ínfimas em comparação ao raio da Terra. Sendo assim todos os corpos analisado terão a mesma direção (vertical) e sentido (para baixo).
A força peso P→ se dá por

Onde P→ e g→ têm a mesma direção e mesmo sentido.
Medida de forças
O dinamômetro é o aparelho utilizado para medir força e sua construção, de maneira mais básica, é baseada em uma mola padrão, que ao sofrer aplicações de forças, teve suas deformações adaptadas a uma escala.
Há uma antiga unidade de força que não pertence ao SI, mas que ainda hoje ocasionalmente é usada: é o quilograma-força, cujo símbolo é kgf. O quilograma-força é definido como a intensidade de força igual à intensidade do peso de um corpo cuja massa é 1 kg, num local onde a aceleração da gravidade tem seu valor normal (9,80665 m/s²).

Sendo assim 1 kgf = 9,80665 N.
TERCEIRA LEI DE NEWTON
Se um corpo A exerce uma força FA→ em um corpo B, então o corpo B exerce uma força FB → em A, tal que: FA→ = -FB→ isto é, as duas forças têm a mesma direção, o mesmo módulo e sentidos opostos.

Para Newton as forças sempre aparecem aos pares e as duas forças que compõem o par se chamam ação e reação.
Dessa forma também podemos entender a terceira Lei de Newton como ele a enunciou: “Para toda ação há sempre uma reação oposta e igual. As ações mútuas de dois corpos entre si são sempre iguais e dirigidas para partes contrárias.”
Convém também destacar que, embora as forças de ação e reação tenham o mesmo módulo, isso não significa que vão produzir acelerações de módulos iguais; a aceleração que cada uma delas produz vai depender da massa de cada corpo, de acordo com a Segunda Lei de Newton.
A Terceira Lei de Newton também é chamada de Lei da Ação e Reação ou Princípio da Ação e Reação.
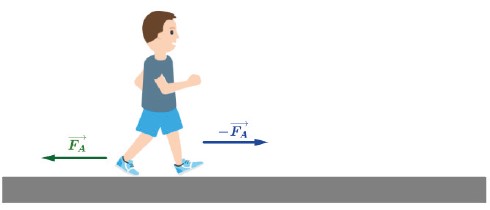
O ato de andar exemplifica bem a ação e reação.
Quando nós empurramos o chão (Terra) para trás, exercendo uma força F→, pelo princípio da ação e reação, o chão nos empurra para frente exercendo uma força de mesmo módulo, mesma direção e de sentido oposto a F→. Dessa forma a nós empurramos a Terra para trás e a Terra nos empurra para frente. Logicamente não há movimento na Terra pois pela segunda Lei de Newton seria necessária uma enorme força para que fosse aplicada uma aceleração na Terra visto sua massa.
Toda vez que tivermos um corpo apoiado sobre uma superfície vamos ter uma força chamada de força de reação FN→.
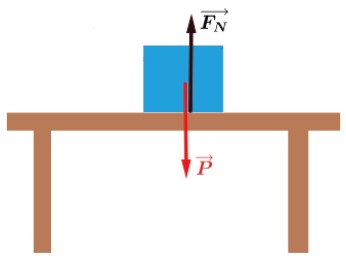
Um erro muito comum é afirmar que a força peso P→ e a força de reação FN→ formam um par de ação e reação. Vamos ver
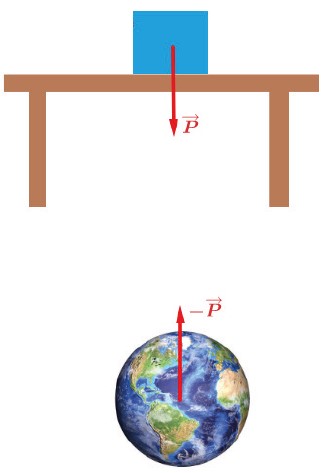
força peso é exercida em relação a Terra. Da mesma maneira que a Terra “puxa” o bloco em sua direção o bloco “puxa” a Terra também mas, como vimos no exemplo de andar, pela massa da Terra é impossível que ela se movimente.
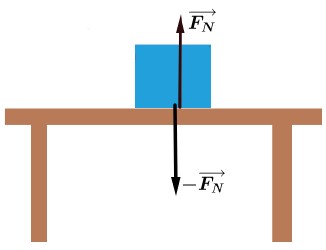
Dessa forma o que é a força normal FN→?
O bloco, ou um corpo de maneira geral, comprime a superfície em que está apoiado, ou nosso exemplo a mesa. Dessa forma a força normal FN→ é a força de reação a essa força de compressão exercida pelo bloco sobre a superfície, que chamaremos de -FN→.
Força de tração
Há diversas situações que as são exercidas através de fios ou cordas. O fio ou corda ideal serão chamados de inextensíveis.
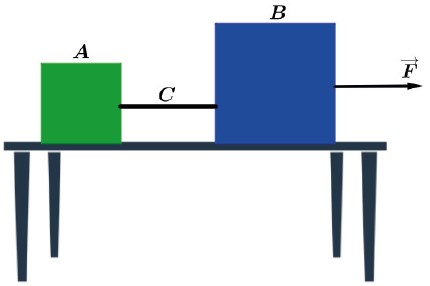
Considere dois blocos A e B, sobre uma superfície lisa sem atrito, unidos por um fio de massa C sendo puxados por uma força F→. Considerando todo o conjunto como um único objeto teremos
F = (mA + mB + mC) · a
Vamos considerar os objetos separadamente
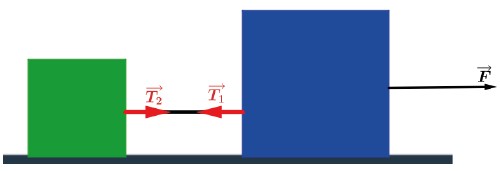
As forças T1→ e T2→ atuantes na corda são as chamadas forças de tração.
A força T2→ “puxa” o bloco A e assim T2 = mA · a
No bloco B temos F→ em uma direção e sentido mas na mesma direção mas em sentido oposto. Assim F – T1 = mB · a
Se analisarmos o fio teremos
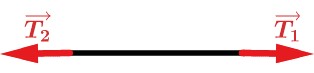
Teremos T1-T2=mC·a
Se tivermos um fio ideal sua massa será desprezível e assim mC = 0
T1 – T2 = mC · a = 0 ⇒ T1 – T2 = 0 ⇒ T1 = T2
Assim, em um fio ideal, as forças de tração nas extremidades são iguais.
A força de tração também pode ser chamada de força de tensão.
Exercício Resolvido 2: (FATEC) No sistema figurado, desprezar dissipação, inércia das rodas e efeitos do ar ambiente. Os carros são interligados por um fio leve, flexível e inextensível.
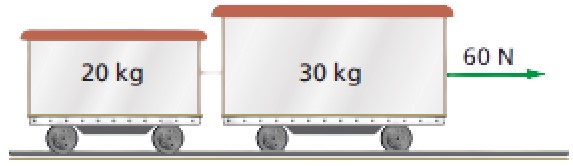
a) A aceleração do carro maior é 2,0 m/s².
b) O sistema move-se necessariamente para a direita.
c) A força de tração no fio de ligação é 24 N.
d) A força de tração da composição, 60 N, transmite-se inalterada para o carro menor.
Resolução:

Se analisarmos a tração do fio que liga os carros, chamando-a de T→ teremos

Não necessariamente o sistema se move para direita. O sistema pode estar se movendo para a esquerda e a força de 60 N “freando” esse movimento imprimindo uma aceleração no sentido contrário do movimento.
Blocos em contato
Considere dois blocos em contato, apoiados em uma superfície perfeitamente lisa com uma força horizontal aplicada a um deles.
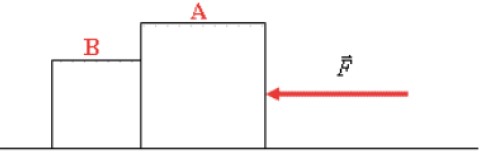
A análise de forças nesses dois blocos terá além da força horizontal, peso, normal e a força de contato entre os blocos, que formam um par de ação/reação.
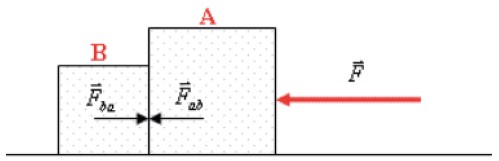
– Na vertical
Bloco A: PA = NA (I)
Bloco B: PB = NB (II)
– Na horizontal
Bloco A: FA = F – FAB = mA · a (III)
Bloco B: FB = FAB =mB · a (IV)
Somando as equações (III) e (IV), podemos encontrar a aceleração do sistema:

Observe que a equação é equivalente a uma força horizontal empurrando um blocão de massa M = mA + mB.
Exercício Resolvido 3: Dois blocos, 1 e 2, são arranjados de duas maneiras distintas e empurrados sobre uma superfície sem atrito, por uma mesma força horizontal F. As situações estão representadas nas figuras I e II abaixo.
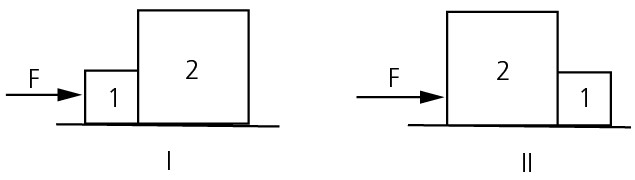
Considerando que a massa do bloco 1 é m1 e que a massa do bloco 2 é m2 = 3m1, a opção que indica a intensidade da força que atua entre blocos, nas situações I e II, é, respectivamente:

Resolução: D
Nos dois casos a aceleração tem mesmo módulo:

EQUILÍBRIO
Dizemos que um ponto material está em equilíbrio quando sua velocidade vetorial se mantém constante. Isso significa que o ponto material permanece em repouso ou em movimento retilíneo uniforme. Quando o ponto material tem velocidade constante e igual a zero, dizemos que está em equilíbrio estático. Quando o ponto material está em movimento retilíneo uniforme, dizemos que está em equilíbrio dinâmico. Para que um ponto material esteja em equilíbrio, é necessário, então, que a resultante das forças que atuam sobre ele seja constante e nula.
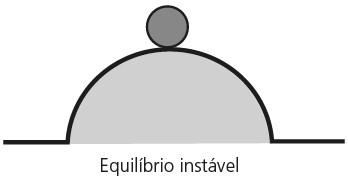
Consideremos um ponto material em equilíbrio estático. Se deslocarmos ligeiramente o ponto material de sua posição de equilíbrio, podem ocorrer três situações:
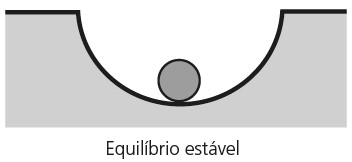
Equilíbrio Estável: Se um objeto, após ser afastado de sua posição de equilíbrio, retornar a ela, dizemos que há equilíbrio estável.
Equilíbrio Instável: Se um objeto, após ser afastado de sua posição de equilíbrio, continuar afastando-se cada vez mais, dizemos que o equilíbrio é do tipo instável.
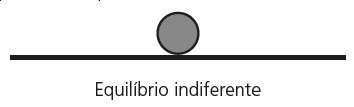
Equilíbrio Indiferente: Quando um objeto tem a sua posição alterada e, mesmo assim, mantém a sua situação de equilíbrio, dizemos que existe o equilíbrio indiferente.