CILINDRO RETO INSCRITO NA ESFERA
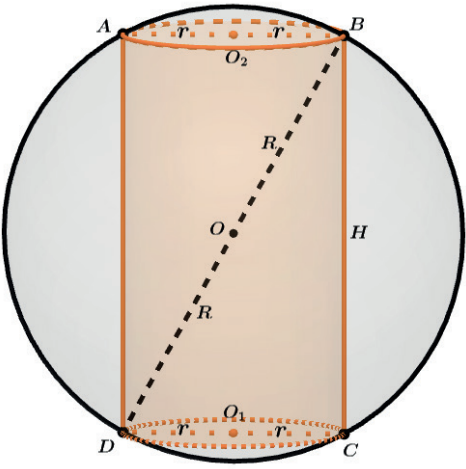
Neste caso podemos fazer a vista frontal e utilizarmos a ideia de um retângulo inscrito num círculo de raio R.
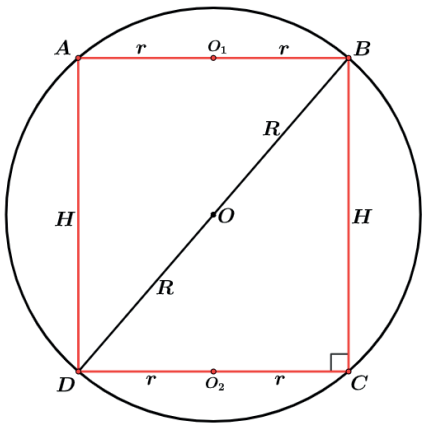
Assim podemos relacionar nossos elementos aplicando o Teorema de Pitágoras no triângulo retângulo BCD.
ProBizu: No caso do cilindro equilátero podemos imaginar o caso do quadrado inscrito no círculo de raio R, onde teremos:
H = 2r ⇒ 4R2 = 4r2 + (2r)2
4R2 = 4r2 + 4r2
4R2 = 8r2
R2 = 2r2
R = r√2
ESFERA INSCRITA NO CONE RETO
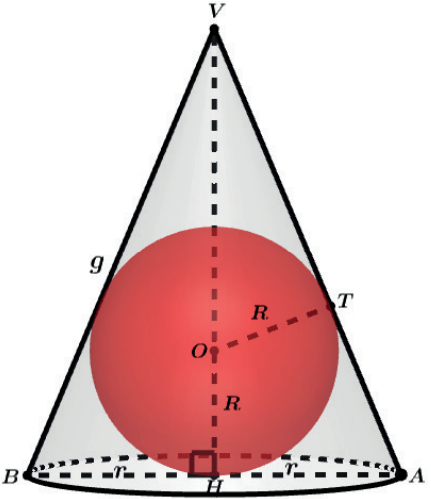
Podemos fazer a assimilação do triângulo circunscrito ao círculo.
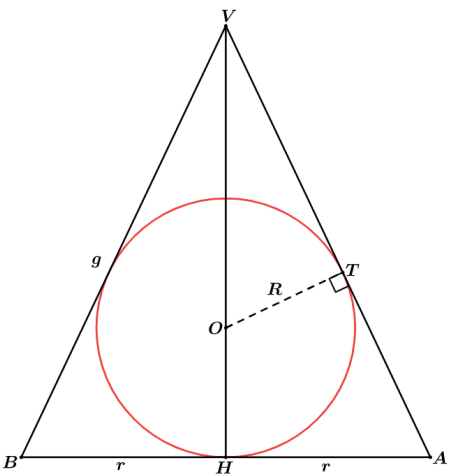
Utilizaremos a fórmula da área do triângulo em função do raio do círculo inscrito SΔ = p ⋅ R, onde poderemos calcular a área do triângulo como SΔ = 2r⋅H/2. No caso analisado os lados do triângulo V A B serão g, g e 2r. Assim:

ProBizu: No caso do cone equilátero podemos imaginar o caso do triângulo equilátero circunscrito ao círculo de raio R:

ProBizu:A esfera só pode ser inscrita no cilindro equilátero.
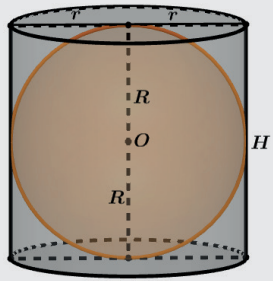
No cilindro equilátero H=2r, assim R = H/2 = r
CUBO INSCRITO NA ESFERA
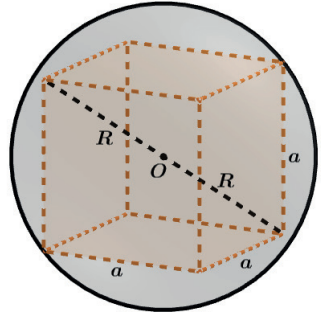
A diagonal do cubo é o diâmetro da esfera, assim 2R = a√3 ⇒ R = a√3/2.
ESFERA INSCRITA NO CUBO
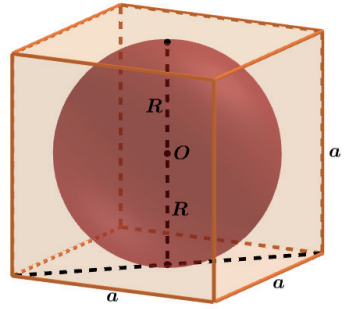
O diâmetro da esfera é igual a aresta do cubo, assim 2R = a ⇒ R = a/2
ESFERA INSCRITA NO TETRAEDRO REGULAR
Seja uma esfera de centro O inscrita em um tetraedro regular VABC como na figura.
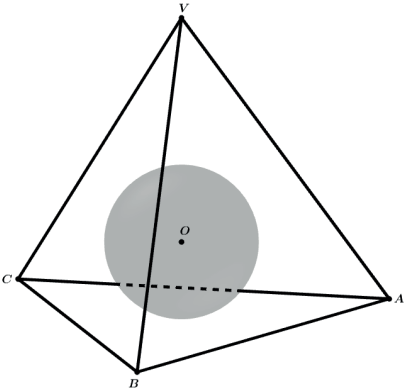
Ao traçarmos as distâncias do centro O da esfera as 4 faces VAB, VAC, VBC e ABC do tetraedro regular teremos todas essas 4 distâncias iguais ao raio da esfera (r).
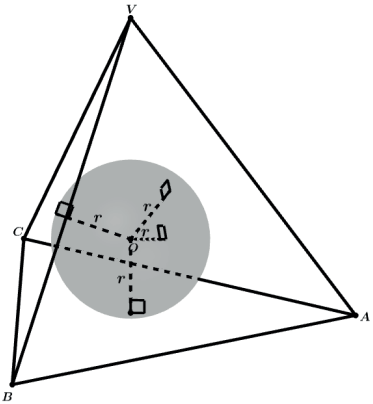
Ao ligarmos o centro O da esfera aos 4 vértices do tetraedro formaremos 4 tetraedros OVAB, OVBC, OVCA e OABC todos de alturas relativas as bases VAB, VBC, VCA e ABC iguais a r.
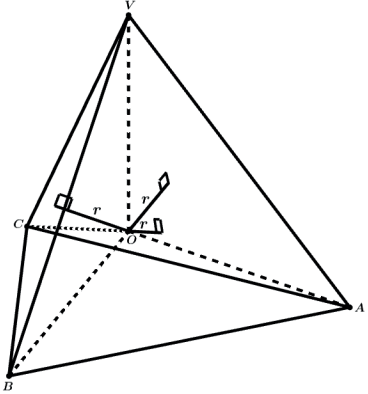
As bases VAB, VBC, VCA e ABC são todas de mesma área, pois são os mesmos triângulos equiláteros que formam o tetraedro regular VABC.
SVAB = SVBC = SVCA = SABC
Assim podemos concluir que o volume do tetraedro VABC pode ser decomposto no volume dos tetraedros OVAB, OVBC, OVCA e OABC.

Perceba que se tivéssemos um ponto P qualquer interior ao tetraedro teríamos as distâncias em relação as 4 faces: d1, d2, d3 e d4. Assim teríamos
1/3 ⋅ SABC ⋅ H = 1/3 ⋅ SABC ⋅ d1 + 1/3 ⋅ SVAB ⋅ d2 + 1/3 ⋅ SVAC ⋅ d3 + 1/3 ⋅ SVBC ⋅ d4
Procedendo de maneira análoga teremos que:
H = d1 + d2 + d3 + d4




