PIRÂMIDE REGULAR INSCRITA EM UM CONE RETO
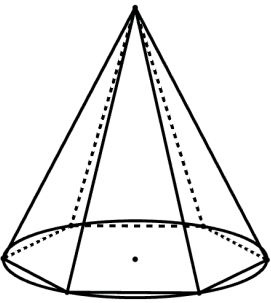
Podemos perceber que ambos os sólidos, pirâmide e cone, possuem a mesma altura (H). Vamos chamar de Scone a área da base do cone e de Spir a área da base da pirâmide.
Sendo assim o volume do cone será Vcone = 1/3 ⋅ Scone ⋅ H enquanto o volume da pirâmide será Vpir = 1/3 ⋅ Spir ⋅ H.
Fazendo a razão entre os volumes do cone e da pirâmide:

A área da base do cone é dada por Scone = π ⋅ R2 e utilizando os polígonos regulares das principais pirâmides regulares teremos os mesmos resultados que os encontrados nos prismas regulares inscritos nos cilindros retos.
- Pirâmide triangular regular inscrita no cone reto

- Pirâmide quadrangular regular inscrita no cone reto

- Prisma triangular regular inscrita no cone reto

CONE RETO INSCRITO EM UMA PIRÂMIDE REGULAR
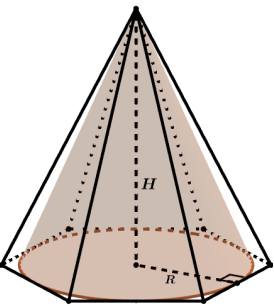
Podemos perceber que ambos os sólidos, pirâmide e cone, possuem a mesma altura (H). Vamos chamar de Scone a área da base do cone e de Spir a área da base da pirâmide.
Sendo assim o volume do cone será Vcone = 1/3 ⋅ Scone ⋅ H enquanto o volume da pirâmide será Vpir = 1/3 ⋅ Spir ⋅ H.
Fazendo a razão entre os volumes da pirâmide e do cone teremos:

A área da base do cone é dada por Scone = π ⋅ R2 enquanto, que para a área da pirâmide podemos utilizar a fórmula da área de um polígono regular Spir = p ⋅ m, onde m é o apótema da base e p é o semiperímetro do polígono. Como neste caso o círculo da base do cone está inscrito no polígono da base da pirâmide teremos que o apótema do polígono será igual ao próprio raio do círculo, assim m = R. Assim:

O que nos faz concluir que a razão entre os volumes é a razão entre os perímetros das bases.
OCTAEDRO FORMADO PELOS CENTROS DAS FACES DE UM CUBO
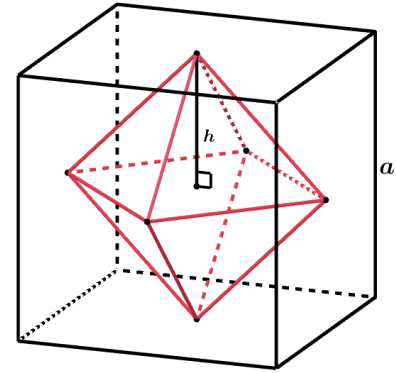
Vamos ligar 2 centros de faces laterais consecutivas do cubo.
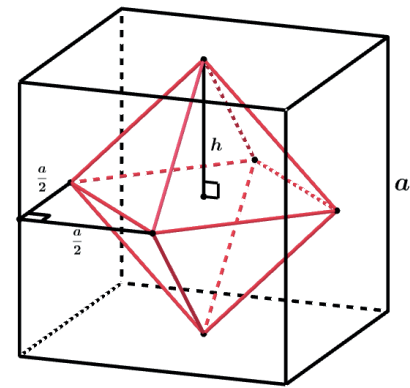
Agora temos o triângulo retângulo indicado na figura e dessa forma podemos calcular a aresta do octaedro regular em função da aresta a do cubo. Vamos chamar a aresta do octaedro regular de x.

Dessa forma o volume do octaedro regular será o dobro do volume de uma das pirâmides quadrangulares regulares que o formam.

É fácil ver que h = a/2, assim:

Isso quer dizer que o volume do octaedro regular é 1/6 do volume do cubo.
CONE RETO INSCRITO NA ESFERA
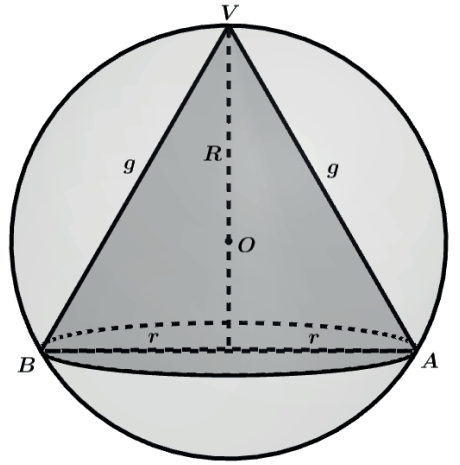
Podemos fazer a assimilação do triângulo inscrito no círculo.
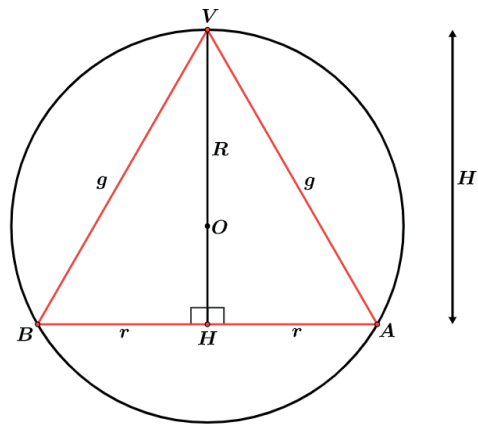
Utilizaremos a fórmula da área do triângulo em função do raio do círculo circunscrito SΔ = abc/4R, onde poderemos calcular a área do triângulo como SΔ = 2r⋅H/2. No caso analisado os lados do triângulo V A B serão g, g e 2r. Assim:

ProBizu: No caso do cone equilátero podemos imaginar o caso do triângulo equilátero inscrito no círculo de raio R:





