PRINCIPAIS POLÍGONOS REGULARES INSCRITOS
PIRÂMIDE REGULAR INSCRITA EM UM PRISMA REGULAR DE MESMA BASE
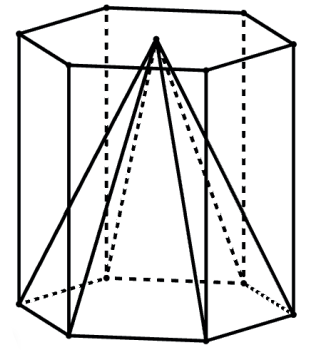
Podemos perceber que ambos os sólidos, pirâmide e prisma, possuem a mesma altura (H) e a mesma área da base. Vamos chamar de Sprisma a área da base do prisma e de Spir a área da base da pirâmide.
Sendo assim o volume do prisma será Vprisma = Sprisma ⋅ H enquanto o volume da pirâmide será V pir = 1/3 ⋅ Spir ⋅ H.
Fazendo a razão entre os volumes do prisma e da pirâmide teremos:

Como o prisma e a pirâmide possuem como bases os mesmos polígonos regulares, teremos que Sprisma = Spir e assim:

A mesma razão é válida para um cone inscrito num cilindro.

PIRÂMIDE REGULAR INSCRITA EM UM PRISMA REGULAR DE BASE DIFERENTE
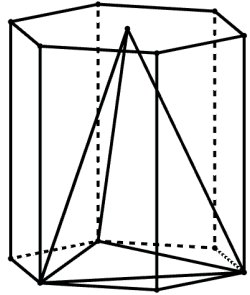
Podemos perceber que ambos os sólidos, pirâmide e prisma, possuem a mesma altura (H). Vamos chamar de prisma Sprisma a área da base do prisma e de Spir a área da base da pirâmide.
Sendo assim o volume do prisma será Vprisma = Sprisma ⋅ H enquanto o volume da pirâmide será V pir = 1/3 ⋅ Spir ⋅ H.
Fazendo a razão entre os volumes do prisma e da pirâmide teremos:

Ou seja, a razão entre os volumes será o triplo da razão entre as áreas das bases.
Vamos mostrar alguns casos
- Pirâmide triangular regular inscrita num prisma hexagonal regular
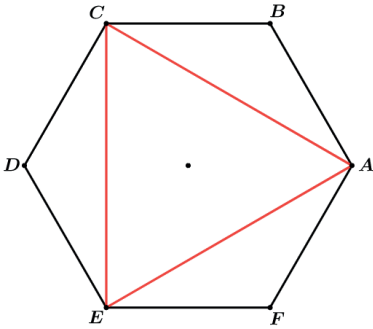
Chamando o lado do hexágono regular ABCDEF de I teremos que o lado do triângulo equilátero ACE será I√3. Fazendo a área do hexágono teremos:

Teremos a área do triângulo equilátero

Assim vemos que a área do hexágono regular é o dobro da área do triângulo equilátero. Sendo o hexágono regular a base do prisma regular e o triângulo equilátero a base da pirâmide regular teremos que Vprisma /Vpir = 3 Sprisma/Spir como Sprisma = 2Spir então Vprisma/Vpir = 3 ⋅ SABCDE/SACE = 3 · 2 = 6.
- Pirâmide quadrangular regular inscrita num prisma triangular regular
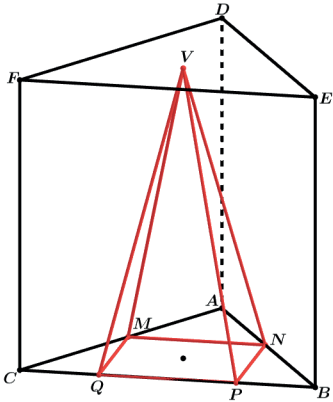
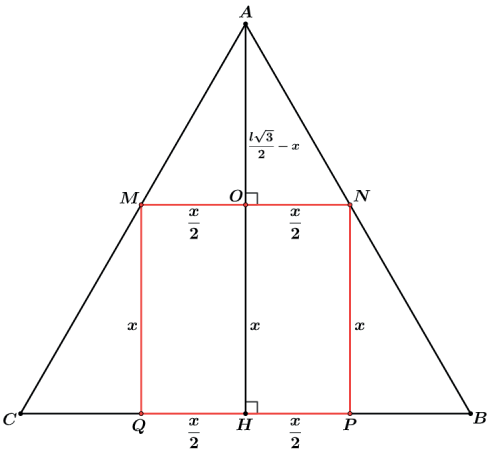
Sendo o lado do triângulo equilátero ABC igual a l e o lado do quadrado MNPQ igual a x montaremos as razões entre os triângulos semelhantes AMN e ABC.

Assim a área do quadrado MNPQ será

Enquanto a área do triângulo equilátero será dada por SABC = I²√3/4
Assim a razão entre os volumes do prisma e da pirâmide será Vprisma/Vpir = 3 Sprisma/Spir como Sprisma = SABC = l²√3/4 2 e Spir = SMNPQ = 31² (7 – 4√3)

PRISMA REGULAR INSCRITO EM UM CILINDRO RETO
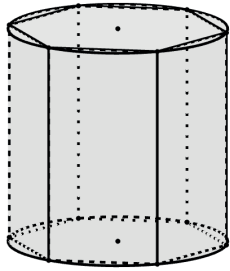
A razão entre os volumes do cilindro reto e do prisma regular inscrito em sua base dar-se-á por

Teremos então que a razão entre os volumes será dada pela razão entre as áreas das bases, que com a ajuda da revisão dos principais polígonos regulares inscritos poderemos definir para os principais prismas regulares retos.
- Prisma triangular regular inscrito no cilindro reto
Scilindro = πR²
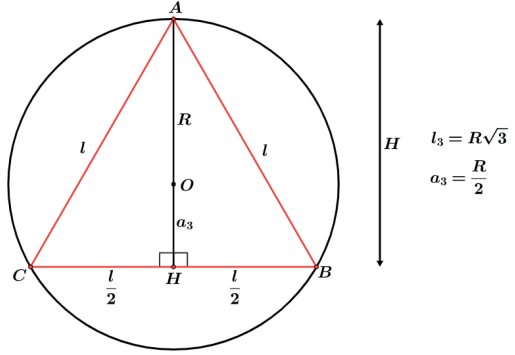
A relação entre o lado do triângulo inscrito e o raio do círculo circunscrito é dado por (figura 1)

- Prisma quadrangular regular inscrito no cilindro reto
Scilindro = πR²
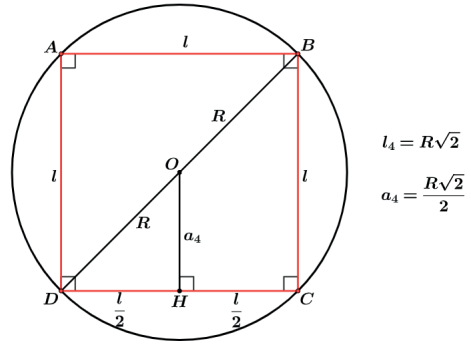
A relação entre o lado do quadrado inscrito e o raio do círculo circunscrito é dado por (figura 2)

- Prisma triangular regular inscrito no cilindro reto
Scilindro = πR²
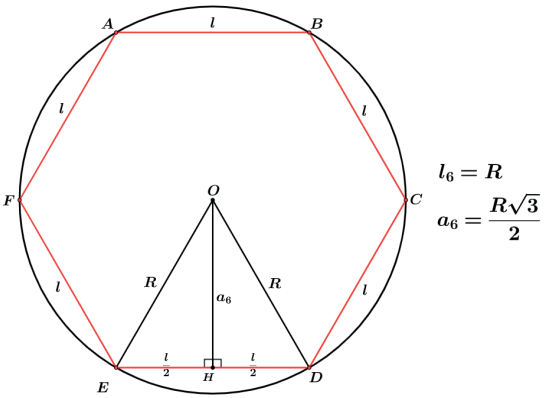
A relação entre o lado do hexágono inscrito e o raio do círculo circunscrito é dado por (figura 3)

PIRÂMIDE REGULAR INSCRITA EM UM CILINDRO RETO
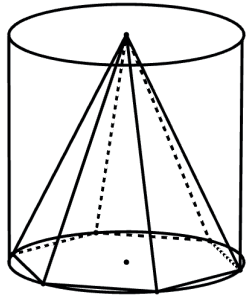
De maneira análoga ao item anterior teremos:

Então vemos que temos o triplo das razões anteriores, assim
- Pirâmide triangular regular inscrita no cilindro reto

- Pirâmide quadrangular regular inscrita no cilindro reto

- Pirâmide triangular regular inscrita no cilindro reto





