INEQUAÇÕES TRIGONOMÉTRICAS
Para simplificar uma inequação trigonométrica são utilizadas as mesmas técnicas utilizadas nas equações trigonométricas., obtendo-se ao final uma inequação básica. Para resolver essa inequação, basta marcar as soluções da “equação” no ciclo trigonométrico e, posteriormente, identificar os intervalos que satisfazem à inequação.
Exemplo:
Resolva a inequação sen x ≤ 1/2 em π [0,2π].
Inicialmente, vamos marcar no ciclo trigonométrico as raízes de:

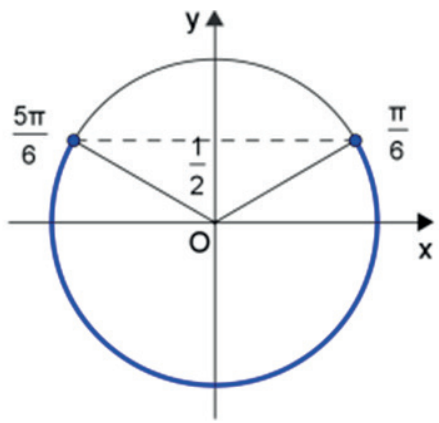
Os valores que satisfazem à inequação são aqueles cujo seno é menor ou igual a 1/2, ou seja:

Vamos ver alguns outros casos
1º caso
Resolver no intervalo 0 ≤ x ≤ 2π, a inequação sen x ≥ 1/2.
Devemos marcar no eixo dos senos os comprimentos maiores que 1/2.
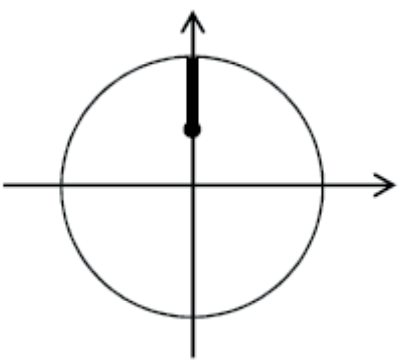
Marcamos na circunferência trigonométrica os pontos que são extremidade final dos arcos x cujo sen x ≥ 1/2.
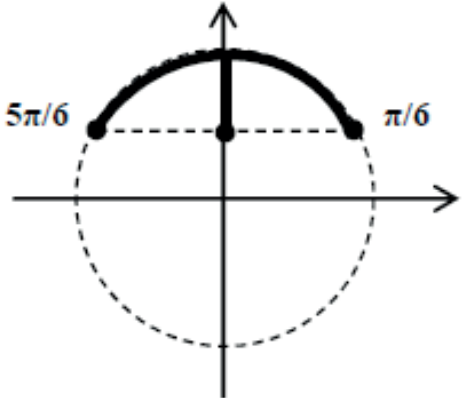

2º caso
Resolver no intervalo 0 ≤ x ≤ 2π, a inequação cosx < √2/2. Devemos marcar no eixo dos cossenos o comprimento menor que √2/2.
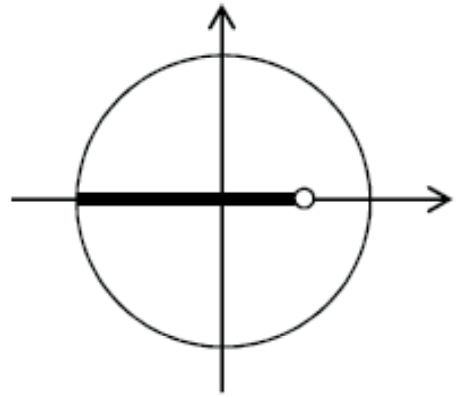
Marcamos na circunferência trigonométrica os pontos que são extremidade final dos arcos x cujo cos x< √2/2.
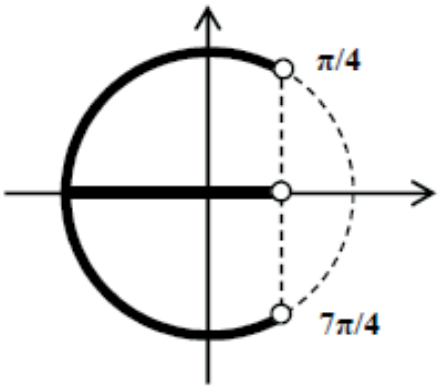

3º caso
Resolver no intervalo 0 ≤ x ≤2π, a inequação sen x< √3/2.
Devemos marcar no eixo dos senos o comprimento menor que √3/2.
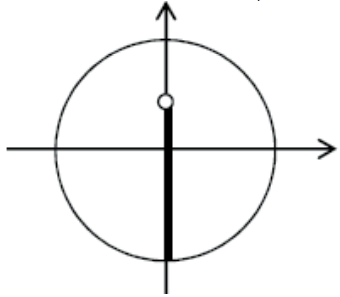
Marcamos na circunferência trigonométrica os pontos que são extremidade final dos arcos x cujo sen x < √3/2.
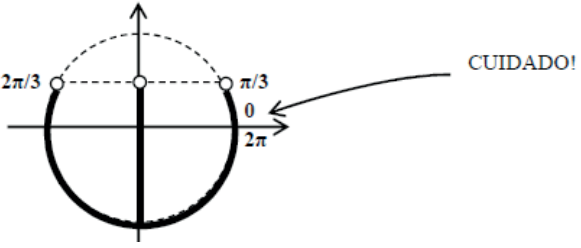
A dificuldade dessa resolução e a maneira de dar a resposta. Para entendermos melhor o porquê da resposta, vamos retificar a circunferência trigonométrica, indicando a resposta gráfica no Universo dado.


SISTEMAS DE INEQUAÇÕES TRIGONOMÉTRICAS
Podemos entender o sistema de inequações também como as inequações simultâneas.
Lembre-se que:

O mesmo vale para as variações de desigualdade ≤.
Assim vamos ver alguns exemplos

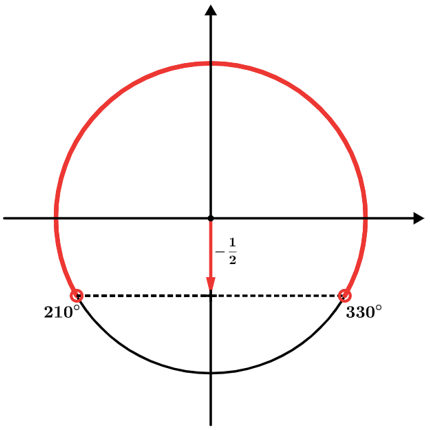
SI = [0°, 210°[U]330°, 360°]
Resolvendo (II)
sen x < √3/2
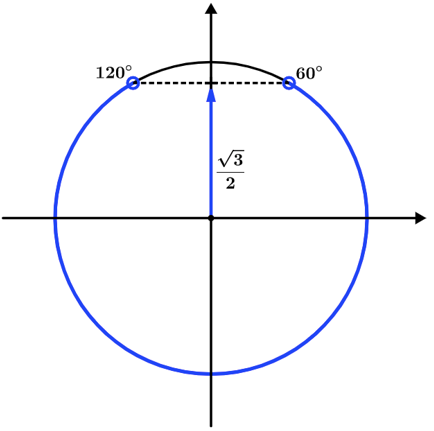
SII = [0°, 60°[U]120°, 360°]
Podemos fazer a intersecção no próprio círculo trigonométrico:

Onde vemos que os arcos comuns as 2 cores são
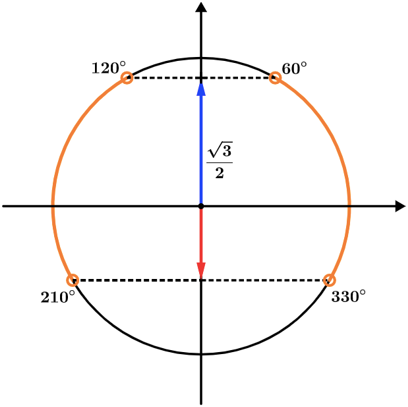
Assim, S = [0°, 60°[U]120°, 210°[U]330°, 360°]. Onde em radianos temos:

O conjunto solução também poderia ser encontrado fazendo intersecção de intervalos reais comumente
S = SI ꓵ SII
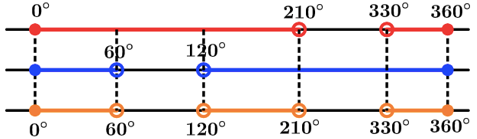

Podemos ter também funções trigonométricas distintas.

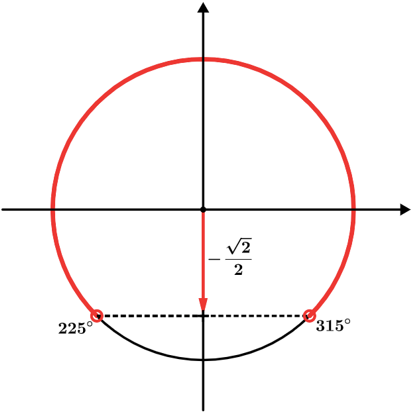
SI = [0°, 225° [U]315°, 360°]
Resolvendo (II):
cos x ≤ √3/2
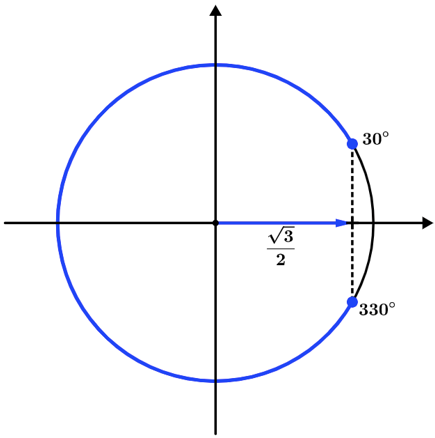
SII = [30°, 330°]
Fazendo a intersecção no próprio círculo trigonométrico teremos:
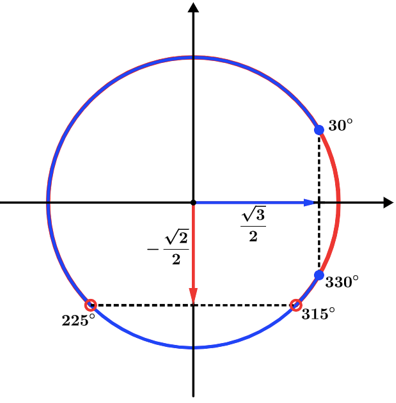
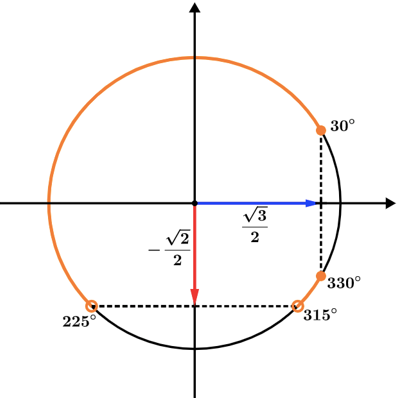
S = [30°, 225°[U]315°, 330°]
Passando para radianos teremos

Vamos ver agora um exemplo um pouco mais elaborado. Qual a solução da inequação 1/4 ≤ cos x · sen x ≤ √2/2, onde x ∈ [0,π]?
Teremos:

Antes vamos fazer o seguinte:

Assim,

Vamos fazer 2x = α e assim:

Vamos analisar primeiro a desigualdade (II).
sen α ≤ √2
Como √2 >1 percebemos que sen α sempre será menor que √2 e assim:
sen α ≤ 2,∀x ∈ ℝ
Assim o que definirá o nosso sistema de desigualdades será a desigualdade (I).
sen α ≥ 1/2
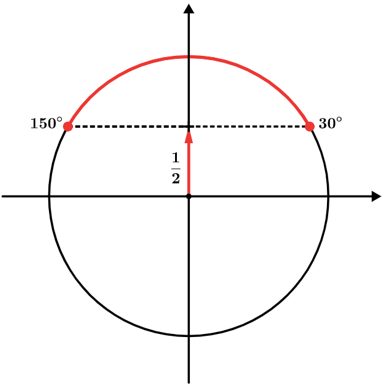
SI = 30° ≤ α ≤ 150°
30° ≤ α ≤ 150°∴ 30° ≤ 2x ≤ 150°∴ 15° ≤ x ≤ 75°
Utilizando os valores em radianos e como já foi visto que a solução da desigualdade (I) será a solução geral teremos:

Lembrando que [15°, 75°] está contido em [0,π].
Vale lembrar que se a questão tivesse dado o intervalo π[0,2π] teríamos:
30° + 360° · k ≤ α ≤ 150° + 360° · k
30° + 360° · k ≤ 2x ≤ 150° + 360° · k
15° + 180° · k ≤ x ≤ 75° + 180° . k
Que no intervalo teríammos:
→Para k=0
15° ≤ x ≤ 75°
→Para k=1
15° + 180° · 1 ≤ x ≤ 75° + 180° · 1
15° + 180° ≤ x ≤ 75° + 180°
195° ≤ x ≤ 255°
Que em radianos:





