EQUAÇÃO
Sejam F e F’ os dois pontos fixos, denominados focos. |FF’| = 2c é a distância focal.
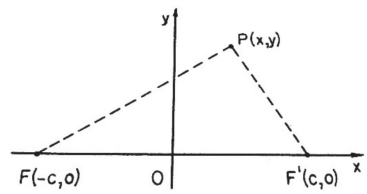
Tomemos para eixo x a reta que passa por F e F’ e para eixo y a mediatriz de FF’ do que resulta: F(–c, o) e F'(c, o).
Chamando P(x, y) o ponto genérico da hipérbole, temos, pela definição:

Por outro lado,

Substituindo na igualdade (1) vem:

Transpondo o segundo radical para o segundo membro, elevando quadrado e simplificando, obtém-se:

Elevando novamente ao quadrado e reduzindo os termos semelhantes vem:

Como c > a, c2 − a2 é um número positivo.
Fazendo c2 − a2 = b2 na equação anterior, tem-se finalmente:

ELEMENTOS DA HIPÉRBOLE
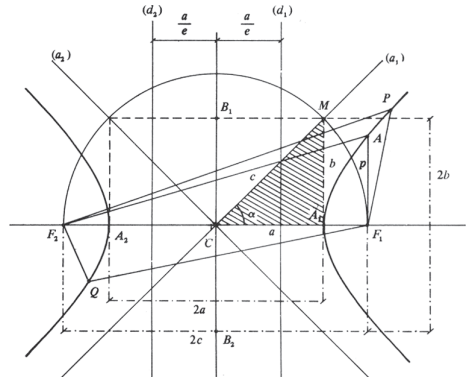
A1 e A2 – vértices
F2 e F1 – focos
C – centro
Eixo real: A2A1 = 2a
Eixo imaginário: B2B1 = 2b
Distância focal: F2F1 = 2c
Raios vetores: F2P→, F1P→
Relações:

Reta: diretrizes são duas retas, (d1) e (d2), perpendiculares ao suporte do eixo real, distando a/e do centro da hipérbole.
Assíntotas são duas retas, (a1) e (a2), que passam pelo centro da hipérbole em posições limites das tangentes a ela, quando os pontos de contato se afastam indefinidamente.
EQUAÇÕES REDUZIDAS
Seja a hipérbole de eixos real A2A1 e imaginário B2B1 com centro na origem. Considere P(x, y) um ponto genérico da curva.
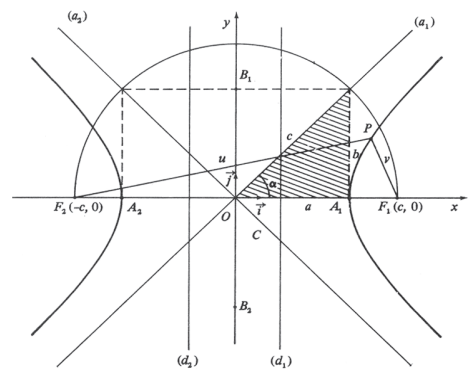

Para y = 0, temos: x = ±a, abscissas dos vértices A1 e A2. Para x = 0, temos: y = ±bi, o que significa que a curva não é interceptada pelo eixo dos y.

A equação da hipérbole de centro na origem, focos no eixo OY e semieixos real e imaginário iguais a a e b é dada por:

As diretrizes são, agora, paralelas ao eixo Ox e suas equações são:

Para y = 0 ⇒ x = ±bi a curva não intercepta o eixo dos x e para x = 0 ⇒ y = ±a, ordenadas dos vértices A1 e A2.
Hipérbole com centro no ponto C(m,n) e A2A1 // Ox.
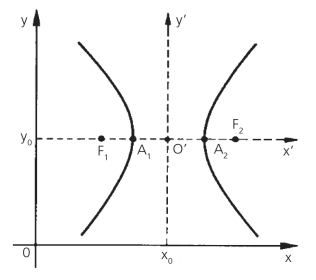
Sua equação é:

As equações das diretrizes são

e das assíntotas

Quando A2A1 // Oy
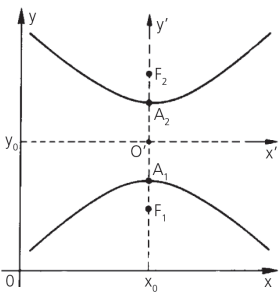


Equação geral: a equação geral é obtida pelo desenvolvimento das formas reduzidas.
HIPÉRBOLE EQUILÁTERA
Uma hipérbole cujos semieixos são iguais (a = b) é chamada de hipérbole equilátera.
As suas equações se simplificam com a substituição de b por a.
POSIÇÕES RELATIVAS ENTRE PONTO E HIPÉRBOLE
Uma hipérbole H e um ponto P, coplanares, têm três posições relativas possíveis, onde 2ª é a medida do eixo real da hipérbole, e F1 e F2 são os focos da hipérbole.
1º caso: P é um ponto da hipérbole.
P ∈ H ⇔ |PF1 − PF2| = 2a
2º caso: P é ponto interior à hipérbole.
P é interior à H ⇔ |PF1 − PF2| > 2a
3º caso: P é ponto exterior à hipérbole.
P é exterior à hipérbole H ⇔ |PF1 − PF2| < 2a
POSIÇÕES RELATIVAS ENTRE RETA E HIPÉRBOLE
Processo prático: seja S o sistema formado pelas equações de r e H. Se, ao substituirmos uma das variáveis da equação de r na equação de H, obtivermos:
I. uma equação do 2º grau com Δ > 0. r e H são secantes;
II. uma equação do 2º grau com Δ ≤ 0. r e H são exteriores;
III. uma equação do 2º grau com Δ = 0. r e H são tangentes.
ProBizu:





