Imagine um recipiente com líquido dentro.
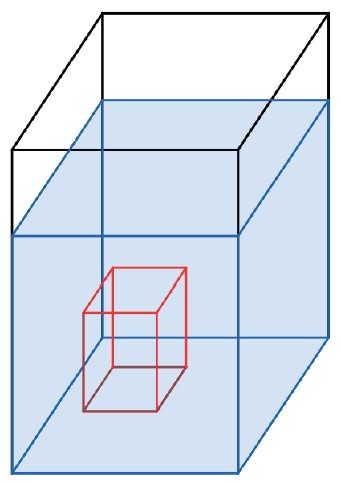
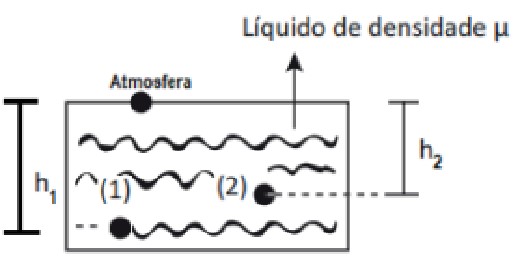
Imagine uma parte desse líquido como por exemplo o sólido interno da figura acima, um paralelepípedo retângulo.
Vamos supor cada face desse paralelepípedo em um nível X e Y respectivamente.
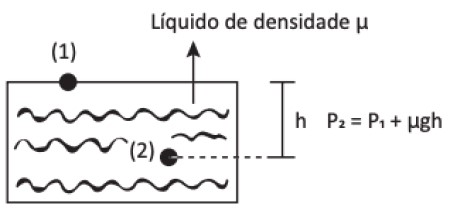
Imaginemos que os pontos X e Y se encontram nos centros das bases, de área A, do paralelepípedo.
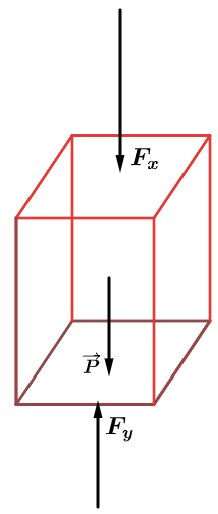
Na face superior do paralelepípedo a pressão é Px e na face inferior é Py. Assim, as forças verticais que o resto do líquido exerce no cilindro têm intensidades
Fx = Px · A e Fy = Py · A
Além dessas duas forças, devemos considerar o peso (P) do cilindro, cujo volume é V. Sendo µ a densidade do líquido, temos:

Para que o cilindro esteja em equilíbrio, devemos ter:
Fy = Fx + P
ou:
Py · A = Px · A + μ · A · h · g ⇒ dividindo toda equação pela área A ⇒ Py = Px + μgh (Lei de Stevin)
Observação: Pontos alinhados dentro de um mesmo fluido, ou na fronteira entre dois fluidos, possuem a mesma pressão, constituindo o que chamamos de linha isobárica.
Para pontos submersos no líquido teremos:

PARADOXO HIDROSTÁTICO
Imagine três recipientes de formatos diferentes, mas todos com bases de mesma área A e contendo um mesmo líquido de altura h.
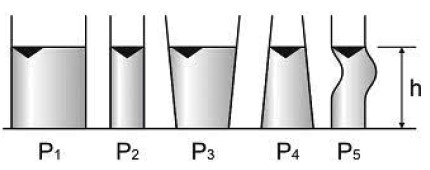
Pela lei de Stevin no fundo de cada um dos três recipientes a pressão é a mesma.
P = Patm + μ · g · h
Como a pressão no fundo de cada recipiente é a mesma e como todos tem a mesma área A teremos que todos tem a mesma força aplicada no fundo do recipiente.
F = P · A
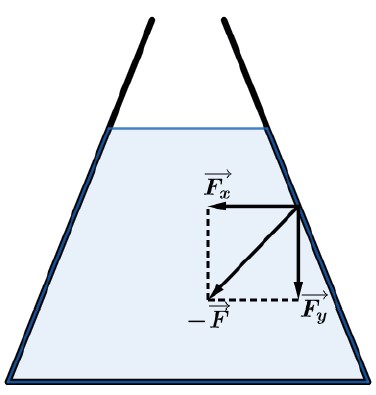
Quando analisamos as forças exercidas pelo líquido no recipiente, como vimos, essas forças são perpendiculares as paredes do recipiente.
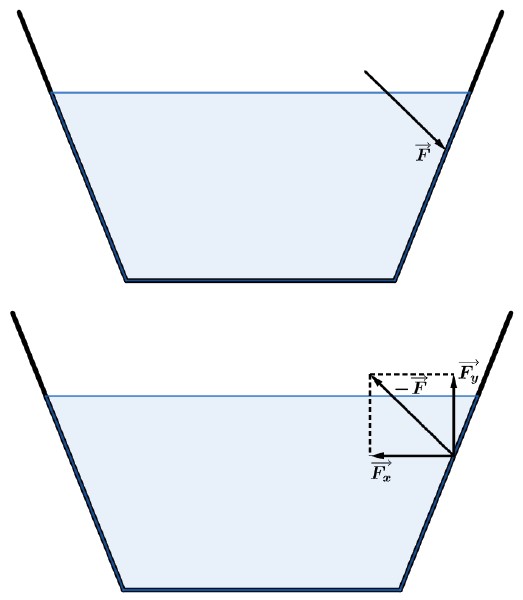
A componente vertical Fy→ é responsável por ajudar a “sustentar” o excesso de líquido (como na figura que supõe um recipiente de abertura superior de área maior que A) e nos recipientes em que a abertura superior é menor que A ela ajuda a comprimir o fundo.