VELOCIDADE DE ESCAPE
Vamos imaginar um foguete saindo da ação gravitacional terrestre (assunto discutido na leitura opcional do módulo anterior). Como o campo gravitacional é conservativo, podemos falar que a energia mecânica do foguete na superfície terrestre é igual a sua energia mecânica quando está a uma distância R → ∞, onde não teria mais a ação gravitacional (“escapou” da Terra).
O problema é que não podemos falar que a energia potencial gravitacional vale mgh, já que a gravidade depende da distância do foguete até o centro da Terra. Quando falamos de um corpo caindo do alto de um prédio, essa preocupação não existe, uma vez que a gravidade é a mesma, tanto no alto do prédio quanto no solo (pensando no ponto mais alto da Terra, o monte Everest, com uma altura de mais de 8 Km, como o raio da Terra é de aproximadamente 6370 km, podemos afirmar que a gravidade é praticamente igual a do nível do mar).
Lembrando que, em um sistema conservativo, temos que:

E que o trabalho da força (que, nesse caso é gravitacional) é dado pela equação abaixo:

Podemos chegar à equação abaixo:

Como essa força aponta para o centro da trajetória e o vetor raio aponta para fora (no caso, da Terra até a posição do foguete), o ângulo entre os vetores vale 180°. Ou seja, após realizar esse produto escalar, aparecerá um sinal negativo, já que cosseno de 180° vale – 1 (produto escalar e vetorial estão discutidos no módulo de vetores. Caso necessário, consulte-o).
Considerando r0 = R (distância inicial entre o foguete e o centro da Terra) e R → ∞, teremos:

Nesse caso, costuma-se tomar a energia potencial no infinito como zero (lembre-se que podemos tomar qualquer ponto como potencial zero. O que interessa é a diferença de energia potencial. Nos casos de queda livre, costumamos considerar potencial zero no ponto mais baixo, geralmente no solo, conforme fizemos no módulo de energia).
Sendo assim, a energia potencial na superfície da Terra vale:

Resolvendo a integral acima chegaremos à expressão abaixo:

Essa é a energia potencial que um corpo de massa m sofre na superfície de outro de massa M. De modo geral, temos que a energia potencial gravitacional de um corpo a uma distância r qualquer em relação ao outro vale:

Note que, conforme um corpo cai em queda livre, a sua energia potencial diminui (aproxima-se da Terra). O sinal de menos acima pode ser explicado pelo fato de, conforme o corpo vai se afastando do planeta, a sua energia potencial deve aumentar, o que, de fato, acontece. O gráfico abaixo mostra isso mais claramente:
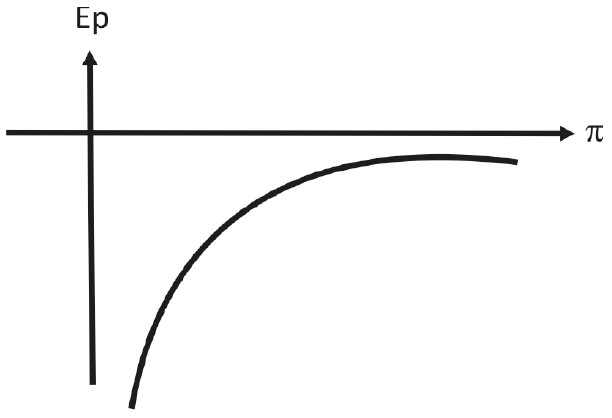
Agora que sabemos a expressão de energia potencial, vamos voltar ao nosso foguete escapando da Terra. Vamos considerar que gastou toda a sua energia para escapar do planeta. Sendo assim, a soma das energias potencial e cinética iniciais do foguete deve ser igual à mecânica final, que é zero. Logo:

Em que ve é a velocidade inicial do foguete, chamada de velocidade de escape. Então:

Podemos substituir com a expressão da gravidade:

No caso da Terra (R ~6,4.106 m), a velocidade mínima para escapar do planeta será:

VELOCIDADE ORBITAL
Qual é o módulo da velocidade que um corpo de massa m tem quando está em órbita a uma distância r de um planeta de massa M? Qual é a velocidade orbital da Terra ao redor do Sol?
Basta lembrarmos que o módulo da aceleração centrípeta é equivalente à gravidade local, gerada por M:

Essa é a velocidade orbital do corpo de massa m. A distância média entre a Terra e o Sol é de aproximadamente 1,5 · 1011 m e M = 2·1030 Kg (massa do Sol). Com esses dados, podemos calcular a velocidade orbital da Terra:

Essa é a velocidade média com que a Terra realiza o seu movimento de translação. Lembrando que é média, já que, quando a Terra está no seu periélio, a velocidade é ligeiramente maior e, quando está no afélio, um pouco menor.
Problema do lixo espacial: milhares de detritos estão, nesse momento, orbitando ao redor da Terra. Objetos de tamanhos variados. A maioria tem poucos centímetros, mas estão em altas velocidades, podendo causar complicações no momento de decolagem ou aterrissagem de uma nave, por exemplo, ou até mesmo destruir uma base ou satélite.
Vamos imaginar um objeto de 10 cm que está a 600 Km da superfície terrestre, ou seja, a aproximadamente 7000 Km do centro da Terra. Sabendo-se que a massa da Terra é de, aproximadamente, 6.1024 Kg, teremos que:

São objetos a incrível velocidade de quase 30.000 km/h! Repare o tempo que esse objeto leva para dar uma volta na Terra:

Após o lixo passar em certo ponto (na verdade, é uma camada de quilômetros de lixo), podemos dizer, de modo aproximado, que há uma janela de 1h30min para atravessar a região.




