1ª LEI DE KEPLER OU LEI DAS ÓRBITAS
“As órbitas descritas pelos planetas ao redor do Sol são elipses, com o Sol em um dos focos”.
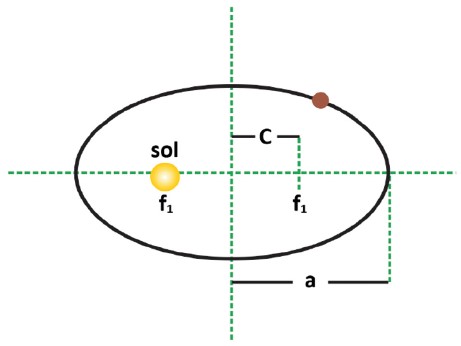
Chamando-se a de semieixo maior e c a semidistância focal, a excentricidade da elipse (e) é e = c/a. Para e = 0, temos um círculo. A excentricidade dos planetas ao redor do Sol é baixíssima. A da Terra, por exemplo, vale 0,017, mostrando o motivo de ter levado muitos a achar que a trajetória era circular. Vênus é o dono da maior excentricidade, 0,206.
Kepler percebeu, também, que o módulo da velocidade dos planetas muda. A velocidade aumenta conforme se aproximam do Sol e diminui conforme vão se afastando, quebrando a ideia de movimento uniforme. Mas, o motivo de isso acontecer, para Kepler, era a atuação de uma força no plano da órbita, tangencial a ela que variasse com o inverso da distância, ou seja, completamente errado (a força é central e varia com o inverso ao quadrado da distância). E, além disso, fez o cálculo errado das áreas varridas pelo raio vetor que liga cada planeta ao Sol. Mas, apesar de todos os erros, conseguiu, com sorte, chegar a um resultado certo.
2ª LEI DE KEPLER OU LEI DAS ÁREAS
“O raio vetor que liga um planeta ao Sol descreve áreas iguais em tempo iguais”.
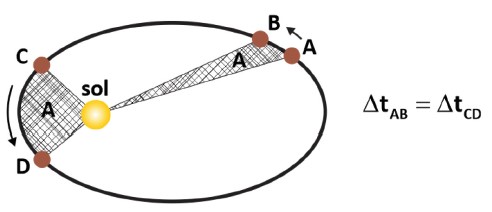
Ou seja, em um mesmo intervalo de tempo, o planeta se deslocaria mais quando estava na região mais próxima em relação ao Sol (periélio) que na região mais afastada (afélio), mostrando que, na região mais próxima a sua velocidade seria maior.
Newton, mais tarde, conseguirá explicar de maneira correta a relação acima. Ele conserva uma grandeza física vetorial chamada de momento angular (L), brevemente discutida no módulo de estática (equilíbrio estático de corpos extensos).
Essa grandeza está intimamente ligada à outra, de natureza escalar, chamada de momento de inércia (I):

Em que ω (= v / r) é a velocidade angular do planeta. Conservando:

O momento de inércia depende do quadrado do módulo de raio vetor r. Sendo assim:
I = krr2
Em que k é uma constante (que depende do formato e da massa do corpo). Então:

Ou seja, se a distância do planeta ao Sol no afélio for 5% maior que no periélio, podemos ver que a sua velocidade, quando estiver no periélio, será 5% maior:
1,05vA = vp
Kepler publicou essas duas leis em seu livro “Astronomia Nova” em 1609. Quase uma década depois, perto da sua morte, publicou a 3ª Lei. Ele sempre tentou buscar uma regularidade com os raios médios das órbitas e o período de revolução dos planetas, até que, em 1618, conseguiu o que tanto buscava:
3ª LEI DE KEPLER OU LEI DOS PERÍODOS
“Os quadrados dos períodos de revolução de dois planetas quaisquer estão entre si como os cubos de suas distâncias médias ao Sol.”
Ou seja:

Na mesma época, outro grande nome que se dedicou à ciência foi Galileu. Aperfeiçoou o telescópio, realizando uma série de descobertas. Verificou que a Lua não era uma esfera perfeita. Apresentava uma série de irregularidades em sua superfície. Descobriu os 4 satélites de Júpiter e mediu os seus períodos de revolução. Descobriu as fases de Vênus (movimento similar ao da Lua, devido ao seu posicionamento relativo ao Sol). Em 1633, foi condenado pela Igreja a ficar em sua casa perpetuamente após se redimir pelos seus “erros e heresias”.
Em 1642, após todas essas descobertas, nasceu Isaac Newton. Não seria possível, neste módulo, falar toda a contribuição de Newton para a ciência; precisar-se-ia de um livro inteiro. Vamos nos ater apenas a algumas das contribuições de Newton na gravitação.
Aplicando a 2ª Lei de Newton em um planeta de massa m que realiza uma trajetória (aproximadamente) circular ao redor do Sol (massa M), temos que:

Esse o módulo da força que o Sol exerce no planeta aponta para o centro da trajetória (resultante centrípeta).
Como:

A relação acima proposta por Kepler é constante para todos os planetas. Logo:

Mostrando, assim, que a força é inversamente proporcional ao quadrado da distância. Além disso, pela 3ª Lei de Newton, a força que o Sol faz em um planeta é igual ao que o planeta faz no Sol, em módulo, concluindo que a sua magnitude depende não só da massa do planeta, mas do produto entre a massa do planeta e a do Sol, chegando à expressão abaixo:

Em que G é a constante universal. Esta é a Lei de Newton da gravitação.
Os estudos de Newton sobre corpos celestes (mecânica celeste) são fascinantes, mas vamos nos restringir, para sermos objetivos, à lei acima.
Podemos inferir, através de sua lei, que a aceleração resultante, que os planetas sofrem devido exclusivamente ao Sol, centrípeta, nada mais é que a gravidade gerada pelo Sol no ponto onde o planeta se encontra. Logo:

Exemplo: Generalizando essa relação, qual seria a gravidade em um ponto a uma distância R (sendo R o raio da Terra) da superfície da Terra (desconsidere a atuação de campos gravitacionais de outros planetas e do Sol nesse ponto)?
Resolução:
Como quem gera o campo gravitacional é a Terra, basta substituirmos a massa do Sol pela da Terra na expressão acima:

Em que:

Perceba que a distância entre o C.M. da Terra e do ponto é 2R. Considerando que o raio médio da Terra é de, aproximadamente, 6370 km, um corpo a 6370 km da superfície da Terra sofre uma gravidade ¼ da superfície da Terra, ou seja, aproximadamente 2,5 m/s².




