Sabemos a expressão da gravidade a uma distância r do centro de um planeta. E, se estivéssemos a uma distância r < R (R = raio do planeta)? Podemos fazer uma analogia com a questão do campo elétrico a uma distância r < R em uma esfera isolante de carga Q. Podemos criar uma espécie de gaussiana, na qual apenas a massa dentro dessa superfície faria campo gravitacional no ponto:
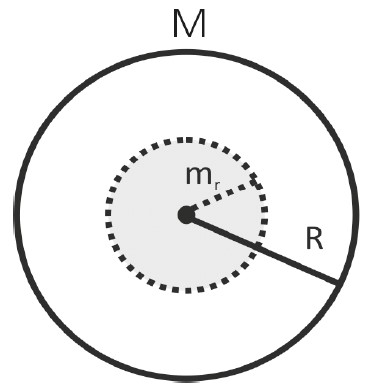
Vamos chamar de m a massa dentro da região pontilhada da figura. Então:

Considerando a densidade do planeta uniforme, temos que:

Logo:

Perceba o caráter linear da função. A gravidade aumenta linearmente com a distância, até que r = R. A partir desse ponto, a gravidade diminui com o inverso do quadrado da distância, caracterizando uma hipérbole, conforme mostra o gráfico g × r abaixo:
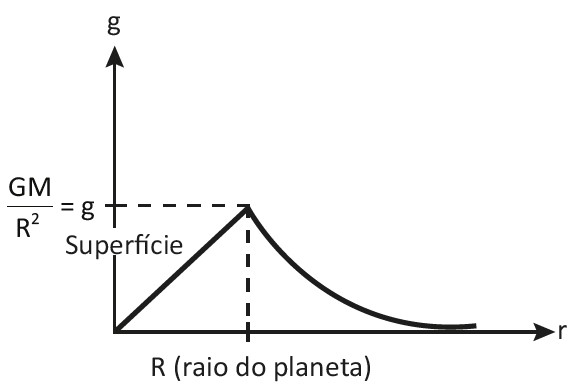
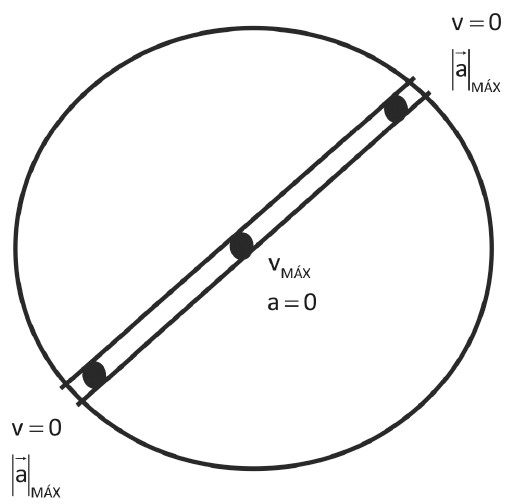
Observação: No interior de um planeta, como a aceleração local é proporcional à distância, se fosse possível cavar um túnel de uma ponta a outra do diâmetro do planeta e colocássemos um corpo de massa m para se locomover ao longo do túnel, o seu movimento seria um M.H.S., cuja velocidade seria zero quando chegasse à superfície e seria máxima no centro do planeta, assim como a aceleração seria máxima na superfície, como vimos, e zero no seu centro.
APÊNDICE
A 3ª lei, R³/T² constante, só faz sentido se a trajetória da partícula for circular. Como sabemos, as trajetórias dos planetas ao redor do Sol, por exemplo, são elípticas, com baixa excentricidade, ou seja, quase circulares. Para a maioria dos exercícios, podemos considerar que as trajetórias são circulares e, caso necessário, basta aplicar a 3ª lei conforme enunciada anteriormente.
Porém, como aplicar a 3ª Lei se as trajetórias forem elípticas?
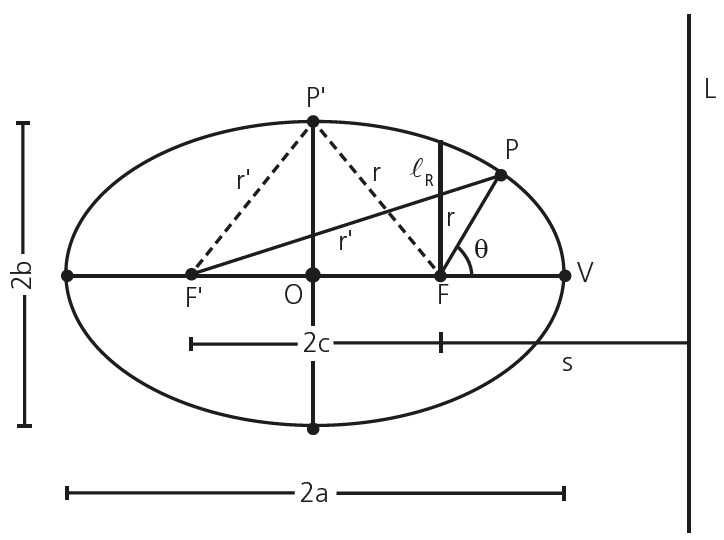
Na figura acima, temos que a é o semieixo maior da elipse. Com um pouco de conta (conhecimento de área de elipse, momento angular e massa reduzida), podemos chegar à relação abaixo (que é a 3ª lei de Kepler):

Conclusão, quanto maior o semieixo maior, maior será o período orbital.
Exercício Resolvido 1: (IME 2010) Três satélites orbitam ao redor da Terra: o satélite S1 em uma órbita elíptica com o semieixo maior a1 e o semieixo menor b1; o satélite S2 em outra órbita elíptica com semieixo maior a2 e semieixo menor b2; e o satélite S3 em uma órbita circular com raio r. Considerando que r = a1 = b2, a1 ≠ b1 e a2 ≠ b2, é correto afirmar que
a) os períodos de revolução dos três satélites são iguais.
b) os períodos de revolução dos três satélites são diferentes.
c) S1 e S3 têm períodos de revolução idênticos, maiores do que o de S2.
d) S1 e S3 têm períodos de revolução idênticos, menores do que o de S2.
e) S2 e S3 têm períodos de revolução idênticos, maiores do que o de S1.
Resolução: D
Como o semieixo maior do satélite 1 tem o mesmo comprimento que o raio da trajetória circular do satélite 3, terão o mesmo período orbital. Já o satélite 2, seu semieixo maior a2 é maior que o semieixo maior que o do satélite 1, logo, terá um período maior que os demais.




