GRÁFICOS DE FUNÇÕES REAIS
Dada uma função na qual seu domínio e contradomínio são subconjuntos dos números reais, o gráfico dessa função é o conjunto de pontos do plano cartesiano (da forma (x, y)) no qual y = f(x).
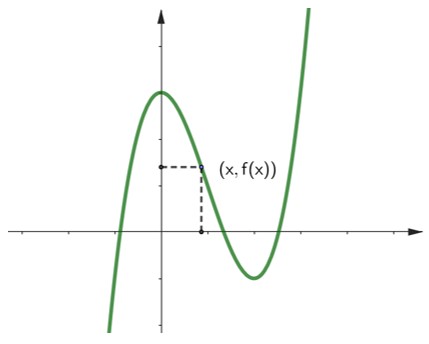
Ou seja, são os pontos do plano onde a coordenada y, é exatamente o valor da função calculada na sua coordenada x.
Exemplo: A figura abaixo representa o gráfico da função f(x) = –x³ – 3x² + 2x + 3
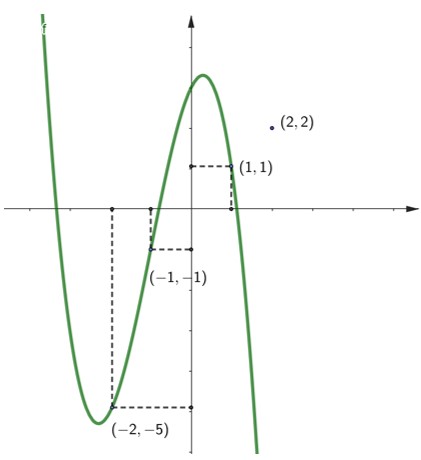
Note que o ponto (1,1) pertence ao gráfico já que f(1) = -1³ – 3 · 1² + 2 · 1 +3 = 1, e o mesmo ocorre para os pontos (–1, –1) e (–2, –5). Já o ponto (2,2) não é um dos pontos do gráfico já que f(2)= –2²- 3 · 2² + 2 · 2 + 3 = -13. Ou seja, para que o ponto esteja no gráfico, a coordenada y deve ser o valor obtido ao substituirmos a coordenada x na função.
É possível também identificar o sinal da função em cada trecho do domínio. Os pontos de imagem positiva encontram-se acima do eixo das abscissas (parte positiva do eixo das ordenadas) e os de imagem negativa abaixo (parte negativa do eixo das ordenadas).
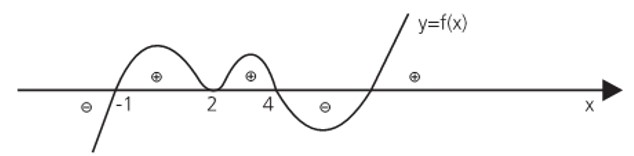
CRITÉRIO PARA RECONHECER FUNÇÕES E RELAÇÕES EM UM GRÁFICO
Nem toda figura no plano cartesiano será o gráfico de uma função, para sabermos se isso ocorre, basta que toda reta vertical corte a função em apenas um ponto.
Exemplo: O gráfico abaixo representa uma função, já que toda reta vertical (retas azuis) cortam esse gráfico em apenas um ponto.
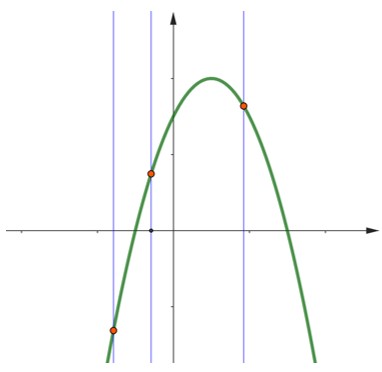
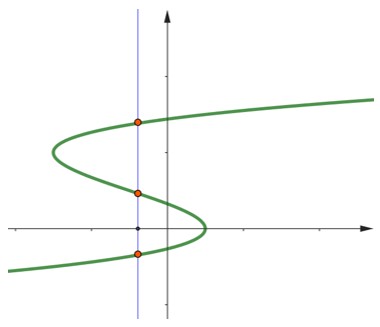
Exemplo: O gráfico abaixo não representa uma função, já que existem retas verticais que cortam esse gráfico em mais de um ponto.
INTERSECÇÃO ENTRE FUNÇÕES
Para saber os pontos nos quais dois gráficos das funções F(x) e G(x) se cruzam, basta resolvermos a igualdade F(x) = G(x).
Exemplo: Quais os pontos de intersecção entre os gráficos das funções f(x) = x³ + 3x + 2 e g(x) = x + 5?
Basta igualarmos

Assim, –3 e 1 são as coordenadas x dos pontos, para acharmos as coordenadas y, basta aplicarmos esses valores de x e uma das funções:
g(-3) = -3 + 5 = 2g(1) = 1 + 5 = 6
Daí, os pontos desejados são (-3,2) e (1,6).




