FÓRMULA TRADICIONAL
A área de um triângulo é igual à metade do produto de um dos lados pela altura relativa a ele.
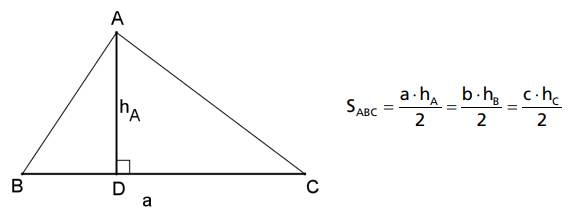
Demonstração:
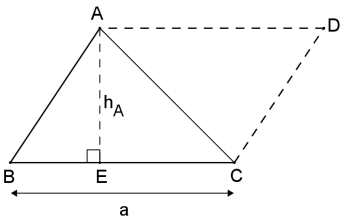
Sejam AD || BC e CD || AB, então o # ABCD é um paralelogramo e ΔABC ≡ ΔCDA(L.L.L .).
Logo:

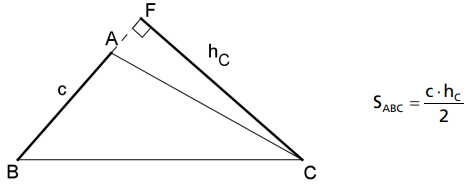
Note que, quando o triângulo é obtusângulo, o pé da altura pode estar no prolongamento do lado, mas a fórmula funciona do mesmo modo.
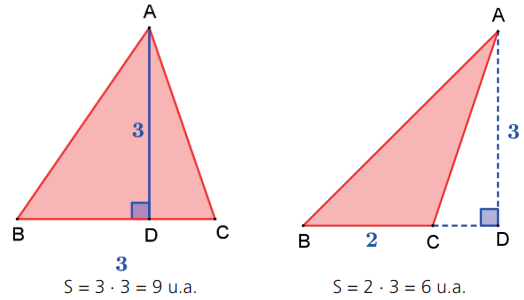
Exemplo: Calcule a área dos triângulos das figuras a seguir.
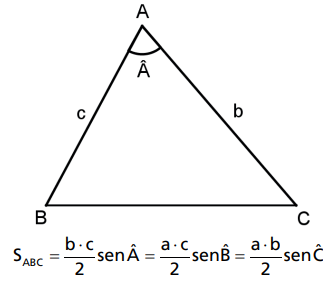
EM FUNÇÃO DO SENO DO ÂNGULO
A área de um triângulo é igual à metade do produto de dois lados adjacentes multiplicado pelo seno do ângulo entre eles.
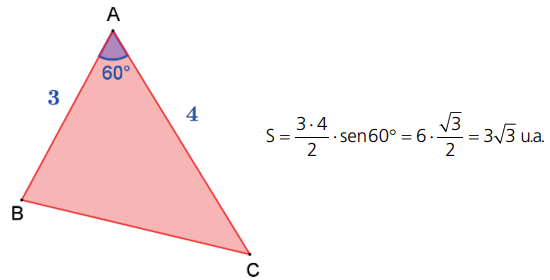
Exemplo: Calcule a área do triângulo da figura a seguir.
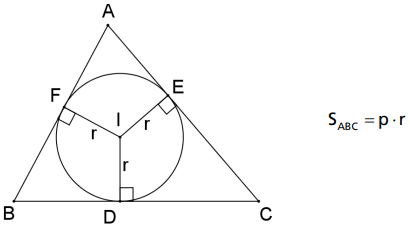
EM FUNÇÃO DO RAIO DA CIRCUNFERÊNCIA INSCRITA
A área de um triângulo é igual ao produto de seu semiperímetro pelo raio do círculo inscrito nesse triângulo.
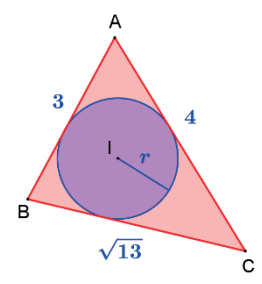
Exemplo: Calcule a área do triângulo da figura a seguir, onde:


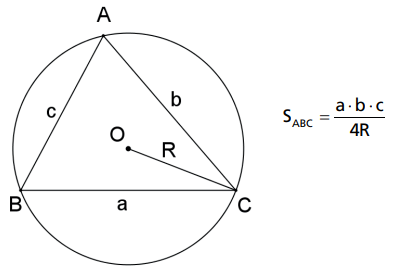
EM FUNÇÃO DO RAIO DA CIRCUNFERÊNCIA CIRCUNSCRITA
A área de um triângulo é igual ao produto dos três lados dividido pelo quádruplo do raio do círculo circunscrito a esse triângulo.
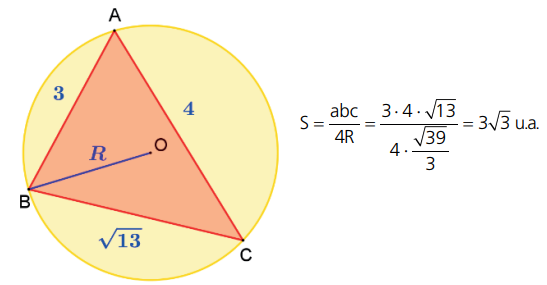
Exemplo: Calcule a área do triângulo da figura a seguir, sabendo que:

FÓRMULA DE HERON
A área de um triângulo é igual à raiz quadrada do produto do semiperímetro pela diferença entre o semiperímetro e cada um dos lados do triângulo.
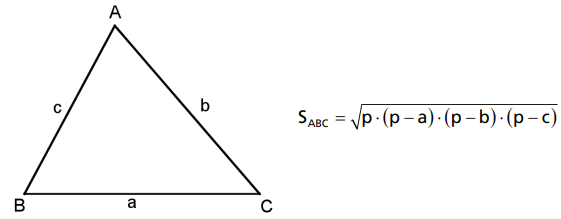
onde p = a+b+c/2 é o semiperímetro do triângulo.
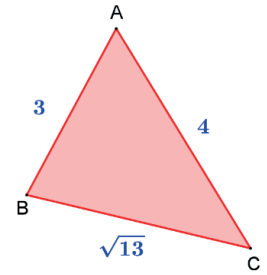
Exemplo: Calcule a área do triângulo da figura.

TRIÂNGULO EQUILÁTERO
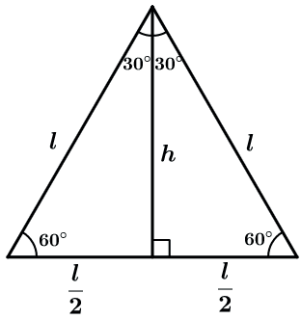
Lembrando que a altura de qualquer triângulo equilátero pode ser calculada como h = l√3/2 , teremos sua área como:

Assim a área de qualquer triângulo equilátero pode ser calculada como l²√3/4.
Exemplo: Calcule a área de um triângulo equilátero que possui o lado medindo √3 cm.
Utilizando a fórmula teremos que a área desse triângulo equilátero será:





