SEMELHANÇA DE TRIÂNGULOS
Se dois triângulos possuem lados respectivamente proporcionais, então são semelhantes.

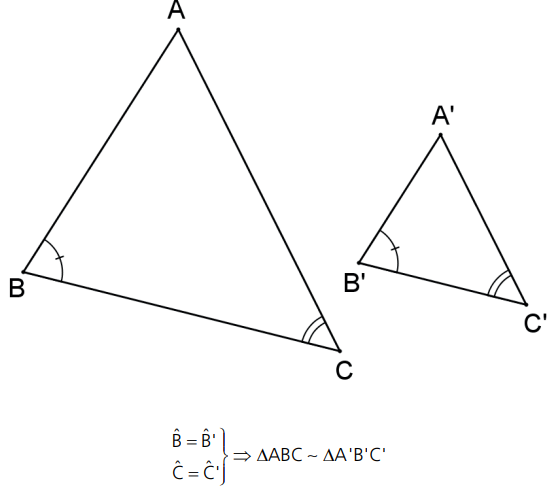
Dois triângulos são semelhantes se, e somente se, seus ângulos são respectivamente congruentes.
Dois triângulos de lados respectivamente paralelos são semelhantes.
Se dois triângulos são semelhantes, então a razão entre duas linhas homólogas é igual à razão de semelhança.
CASOS DE SEMELHANÇA DE TRIÂNGULOS
1° caso: (A.A.) Se dois triângulos possuem dois ângulos respectivamente congruentes, então são semelhantes.
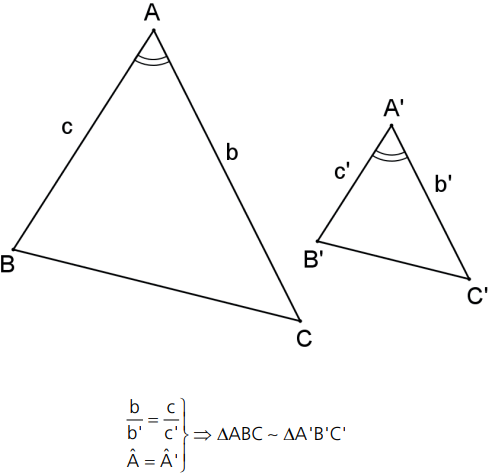
2° caso: (L AL p p ) Se dois triângulos possuem dois lados proporcionais adjacentes a ângulos congruentes, então são semelhantes.
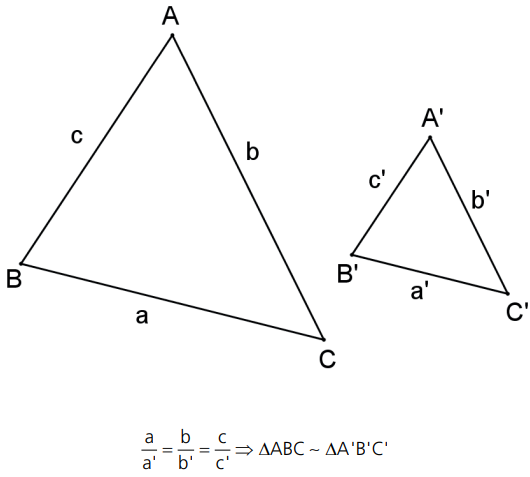
3° caso: (LLL ppp ) Se dois triângulos possuem os três lados respectivamente proporcionais, então são semelhantes.
Exemplo: Considere os quadrados da figura de lados a e b (a > b). Então x é igual a
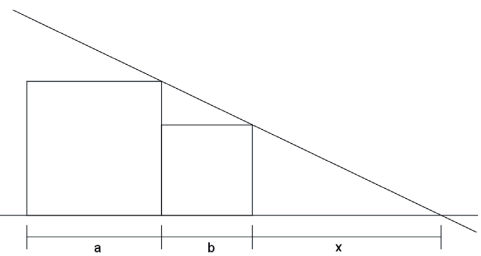

Resolução:
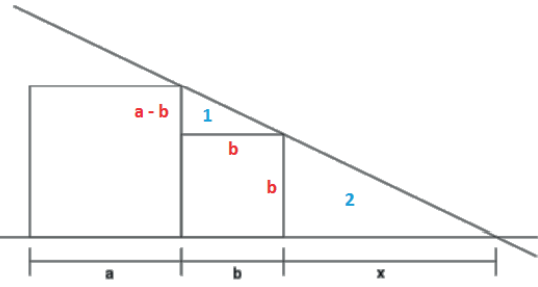
Os triângulos retângulos “1” e “2” possuem lados paralelos, logo são semelhantes.
Assim, temos:

ProBizu
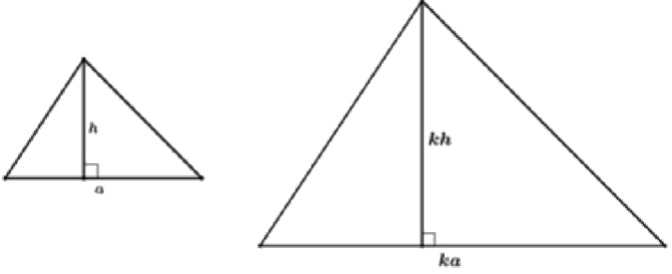
Quando utilizamos a semelhança de figuras planas aplicada a dimensões lineares (de comprimento) temos uma razão k de semelhança porém quando aplicamos a razão de semelhança em relação as áreas das figuras a nossa razão passa a ser k².
Temos 2 triângulos semelhantes de razão de semelhança k.
Nosso triângulo da esquerda possui área SI = a·h/2 enquanto o nosso triângulo da direita possui área:

Sendo assim fica claro que sempre que fizermos uma razão de semelhança entre áreas a razão que deve ser utilizada é k².




