RELAÇÕES MÉTRICAS NOS POLÍGONOS REGULARES
TRIÂNGULO EQUILÁTERO INSCRITO
O lado de um triângulo equilátero (regular) inscrito em uma circunferência de raio R é I3 = R√3e o seu apótema é a3 = R/2.

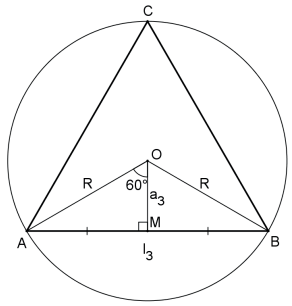
Demonstração:
No triângulo retângulo AOM da figura temos:

QUADRADO INSCRITO
O lado de um quadrado (quadrilátero regular convexo) inscrito em uma circunferência de raio R é I4 = R√2 e o seu apótema é a4 = R√2/2.

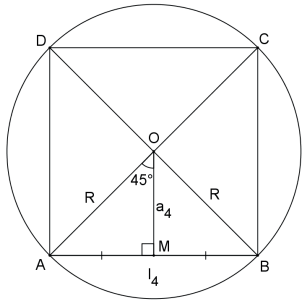
Demonstração:
No triângulo retângulo AOM da figura temos:

Poderíamos observar também que o triângulo da figura é um triângulo retângulo isósceles e, portanto, a4 = l4/2.
HEXÁGONO REGULAR CONVEXO INSCRITO
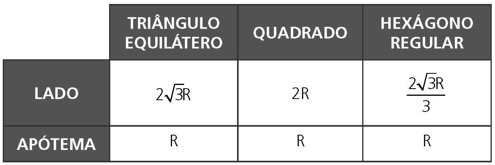
O lado de um hexágono regular convexo inscrito em uma circunferência de raio R é I6 = R e o seu apótema é a6 = a√3/2.

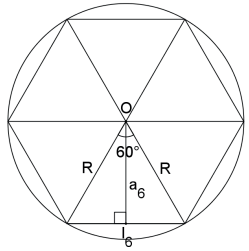
Demonstração:
O hexágono regular pode ser dividido em seis triângulos equiláteros. Dessa forma, o lado de cada triângulo equilátero é I6 = R e o apótema é igual à altura desse triângulo a6 = R√3/2.

TRIÂNGULO EQUILÁTERO CIRCUNSCRITO
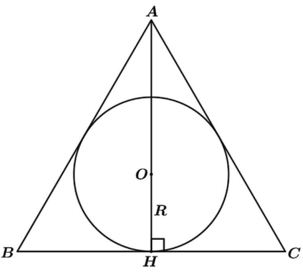

QUADRADO CIRCUNSCRITO
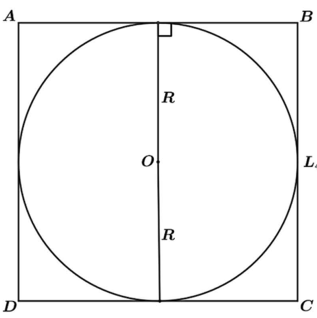
É fácil ver pela figura que L4 = 2R e A4 = R.
HEXÁGONO REGULAR CIRCUNSCRITO
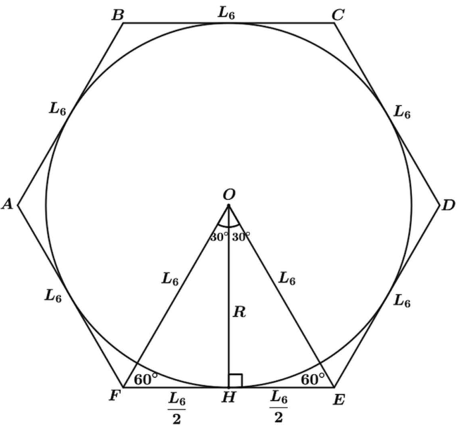

OCTÓGONO REGULAR CONVEXO



Demonstração:
Vamos utilizar a fórmula de duplicação de gênero desenvolvida anteriormente:

Assim, temos:

Utilizando agora a expressão para o cálculo do apótema:


DECÁGONO REGULAR CONVEXO
O lado de um decágono regular convexo inscrito em uma circunferência de raio:


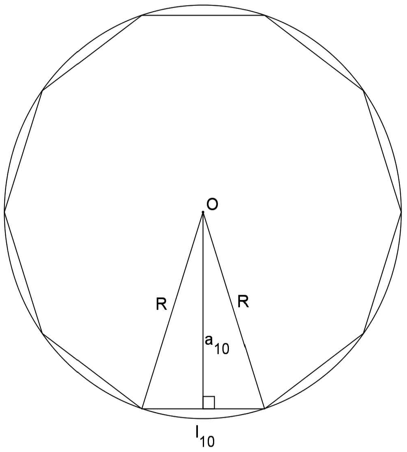
Demonstração:
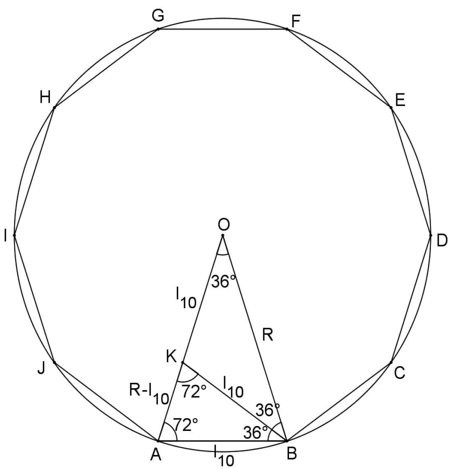

PENTÁGONO REGULAR CONVEXO
O lado de um pentágono regular convexo inscrito em uma circunferência de raio:


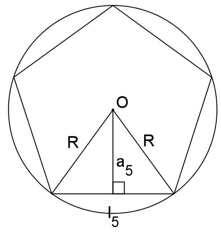
Demonstração:
Na figura da demonstração do lado do decágono regular, vamos aplicar a lei dos cossenos ao ∆OAB. Assim, temos:

Voltando à figura do pentágono, consideremos o triângulo retângulo OAM. Assim, temos:

Aplicando o teorema de Pitágoras a esse triângulo, temos:

DODECÁGONO REGULAR CONVEXO
O lado do dodecágono regular convexo inscrito em uma circunferência de raio:

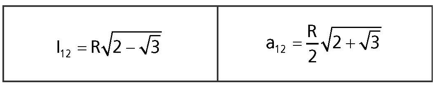
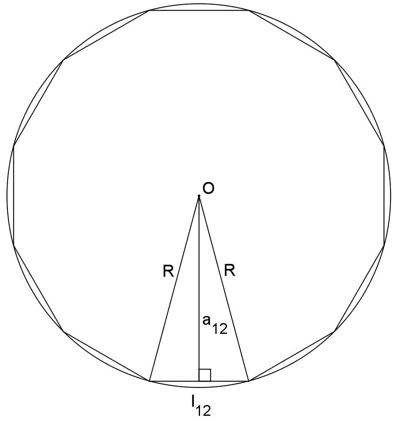
Demonstração:
Vamos utilizar a fórmula de duplicação de gênero desenvolvida anteriormente:

Utilizando agora a expressão para o cálculo do apótema:


OUTRAS PROPRIEDADES GEOMÉTRICAS IMPORTANTES
RETA DE SIMSON-WALLACE
Se perpendiculares são traçadas a partir de um ponto sobre o circuncírculo de um triângulo a seus lados, suas interseções com os lados do triângulo são colineares e pertencem à Reta de Simson-Wallace. (A recíproca também é verdadeira.)

RETA DE EULER
Num triângulo ABC, o ortocentro (H), o baricentro (G) e o circuncentro (O) são colineares.
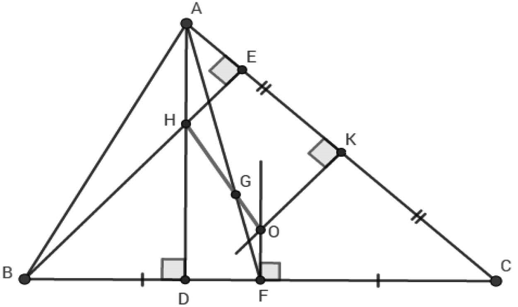
Além disso uma consequência importante é que a razão AH : OF é igual a 2 : 1 também. E além disso o baricentro (G) divide o segmento HO na razão 2 : 1.
CÍRCULO DE NOVE PONTOS
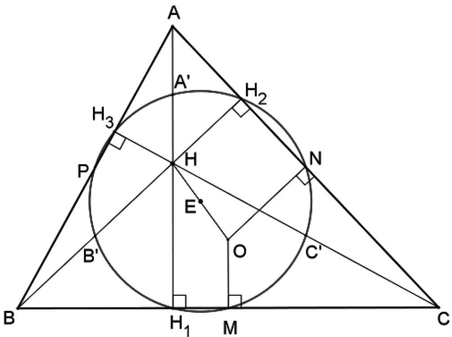
Num triângulo ABC, sejam M, N e P os pontos médios dos lados BC, AC e AB. Sejam H1, H2 e H3 os pés das alturas de A, B e C, e seja H ortocentro de ABC. Sejam ainda A’, B’ e C’ pontos médios dos segmentos AH, BH e CH. Tem-se então que os pontos M, N, P, H1, H2, H3, A’,B’ e C’ são concíclicos, ou seja, existe uma circunferência passando por todos esses pontos. O centro dessa circunferência é o ponto médio do segmento OH, que liga o circuncentro O ao ortocentro H do triângulo ABC.
TEOREMA DE CARNOT
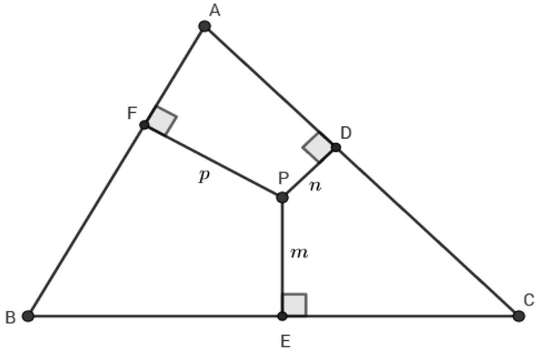
Sobre os lados BC, AC e AB de um triângulo ABC, tomam-se os pontos D, E e F, respectivamente. Tem-se que as perpendiculares em D, E, F aos lados aos quais eles pertencem são concorrentes se, e somente se,





