Geometria Plana: Relação de Stewart

A relação de Stewart é um teorema importante na geometria que relaciona as medidas dos lados de um triângulo com a medida de uma ceviana (segmento que liga um vértice a um ponto no lado oposto). Essa relação é útil para resolver problemas de geometria analítica e é uma extensão do Teorema de Pitágoras.

Seja um triângulo ABC de lados B̲C̲ = a, A̲C̲ = b e A̲B̲ = c, e a ceviana A̲P̲ = x que divide o lado B̲C̲ em dois segmentos B̲P̲ = n e C̲P̲ = m, então

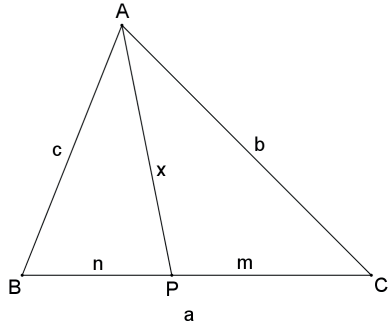
c²m + b²n = x²a + amn

Demonstração:

Seja AP^B = θ, então A P^C =180° − θ. Aplicando a lei dos cossenos aos triângulos APB e APC, temos:

Exemplo:

Calcule x na figura abaixo

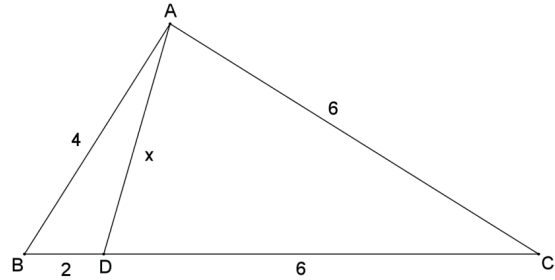
Resolução:

Pela relação de Stewart, temos:

4² . 6 + 6² . 2 = x² . 8 + 8 . 2 . 6 ⇔ 9x² = 72 ⇔ x² = 9 ⇔ x = 3