Geometria Plana: Quadrilátero circunscritível

Um quadrilátero circunscritível é um quadrilátero que pode ser inscrito em uma circunferência de tal forma que todos os vértices do quadrilátero pertencem à circunferência. Isso resulta em ângulos especiais e relações geométricas únicas que são exploradas na geometria, especialmente em problemas de construção e cálculo de áreas.

Teorema de Pitot: Um quadrilátero convexo é circunscritível se, e somente se, as somas das medidas dos lados opostos são iguais.

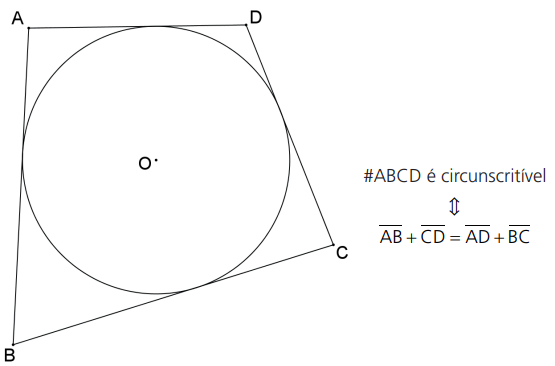
Exemplo:

Determine o perímetro do quadrilátero circunscritível ABCD da figura.

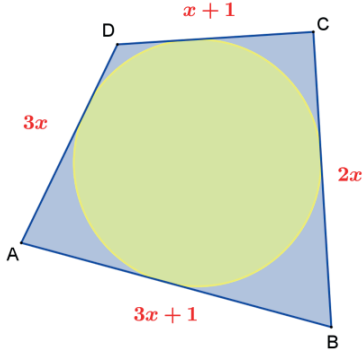
Resolução:

Como o quadrilátero ABCD é circunscritível, então as somas dos lados opostos são iguais. Assim, temos:

Portanto, o perímetro do quadrilátero é 2p_ABCD = (3x + 1) + 2x + (x + 1) + 3x = 9x + 2 = 9 ⋅ 2 + 2 = 20.