PROPRIEDADE DA TANGENTE
Uma reta é tangente a uma circunferência se, e somente se, é perpendicular ao raio no ponto de tangência.
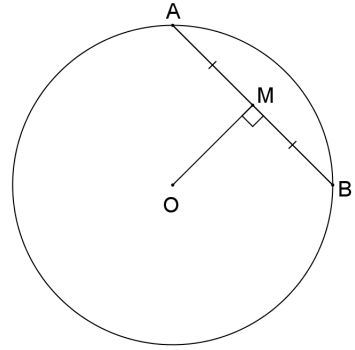
Exemplo:
Calcule o comprimento do segmento tangente a uma circunferência de raio 3 cm traçado a partir de um ponto que dista 5 cm do centro dessa circunferência.
Resolução:
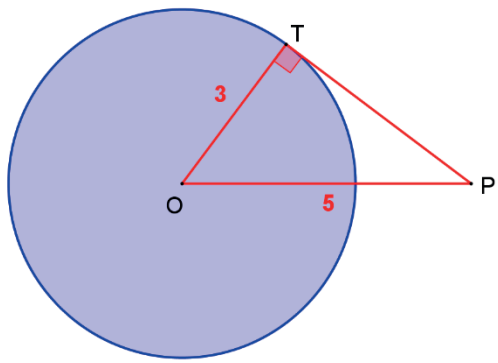
Seja P̲T̲ um segmento de reta tangente à circunferência, então P̲T̲ ⊥ O̲T̲.
Aplicando o teorema de Pitágoras no triângulo retângulo OPT, temos:

SEGMENTOS TANGENTES
Os segmentos tangentes a uma circunferência, traçados por um ponto exterior a ela, são congruentes.
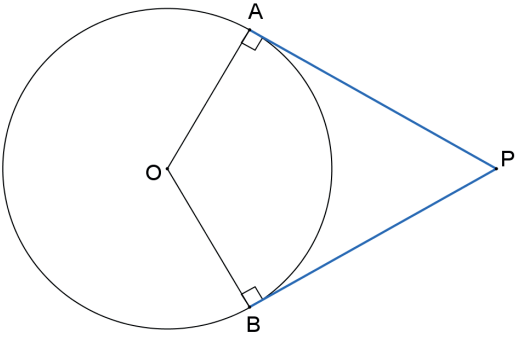
Demonstração:

(caso especial de congruência de triângulos retângulos) ⇒ P̲A̲ = P̲B̲
ProBizu:
O raio do círculo inscrito em um triângulo retângulo é igual ao semiperímetro menos a hipotenusa.
Seja um triângulo retângulo ABC de hipotenusa B̲C̲ = a e semiperímetro p, então o raio do círculo inscrito é r = p – a.
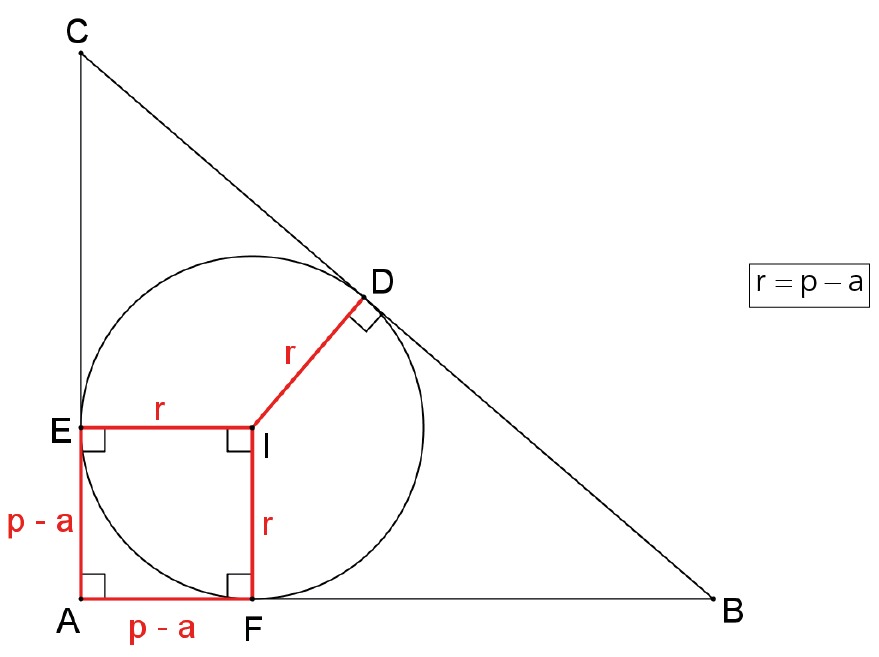
Exemplo:
Calcule o perímetro de um triângulo retângulo de hipotenusa 5 cm e raio do círculo inscrito 1 cm.
Resolução:
Sabemos que o raio r do círculo inscrito em um triângulo retângulo de semiperímetro p e hipotenusa a é dado por r = p – a.
Substituindo os valores dados no enunciado, temos: 1 = p – 5 ⇔ p = 6.
Logo, o perímetro do triângulo retângulo é 2p = 2 ⋅ 6 = 12 cm.




