Propriedade da secante
Seja uma reta s secante a uma circunferência λ de centro O e raio r, que não passa por O e que intercepta a circunferência nos pontos A e B distintos. O ponto M é o ponto médio da corda A̲B̲ se, e somente se, O̲M̲ ⊥ A̲B̲.
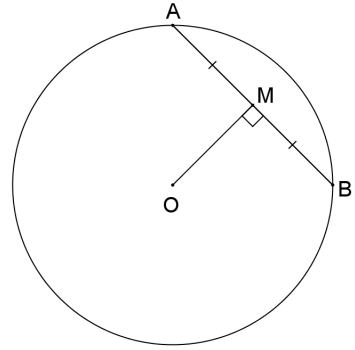
Demonstração:
Supondo que o ponto M seja ponto médio de A̲B̲, então ΔOMA ≡ ΔOMB (L.L.L.), o que implica AM^O = BM^O 90°.
Supondo que O̲M̲ ⊥ A̲B̲, então ΔOMA ≡ ΔOMB (L.L.L.) (O̲M̲ comum e O̲A̲ = O̲B̲, caso especial de congruência para triângulos retângulos), o que implica A̲M̲ = M̲B̲.
Exemplo:
Calcule o comprimento de uma corda que dista 3 cm do centro de uma circunferência de raio 5 cm.
Resolução:
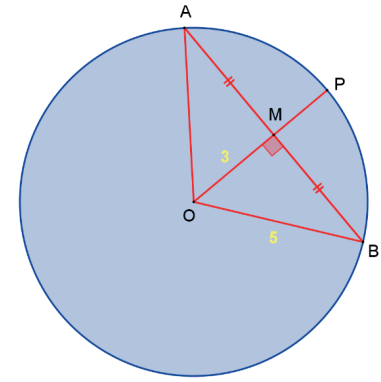
Seja A̲B̲ a corda em questão e O̲M̲ ⊥ A̲B̲, então O̲M̲ = 3 e M é ponto médio de A̲B̲, ou seja, A̲M̲ = M̲B̲.
Aplicando o teorema de Pitágoras ao triângulo retângulo OMB, temos:

Logo, A̲M̲ = B̲M̲ = 4 e A̲B̲ = 8 cm.




