Posições relativas entre reta e circunferência
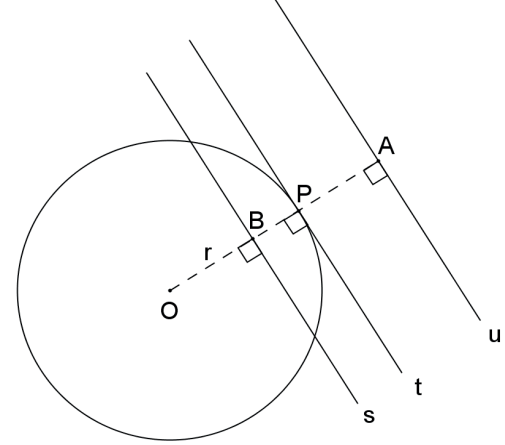
A reta s é secante à circunferência de centro O e raio r se, e somente se, a distância do centro da circunferência à reta é menor do que o raio: d(O, s) < r.
A reta t é tangente à circunferência de centro O e raio r se, e somente se, a distância do centro da circunferência à reta é igual ao raio: d(O, t) = r.
A reta u é exterior à circunferência de centro O e raio r se, e somente se, a distância do centro da circunferência à reta é maior do que o raio: d(O, u) > r.
Exemplo:
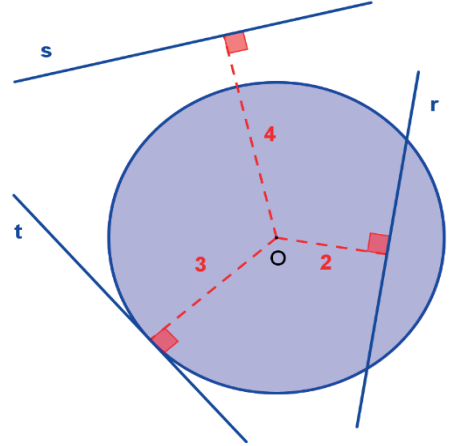
Seja uma circunferência de centro O e raio R = 3. Identifique a posição relativa entre as retas r, t, s e a circunferência, sabendo-se que as distâncias entre as retas e o centro da circunferência são, respectivamente, d(O, r) = 2, d(O ,t) = 3 e d(O, s) = 4.
Resolução:
A reta r é secante à circunferência, pois d(O, r) = 2 < 3 = R.
A reta t é tangente à circunferência, pois d(O, t) = 3 = R.
A reta s é exterior à circunferência, pois d(O, s) = 4 > 3 = r.
Veja a figura a seguir, na qual essas retas estão representadas.