Posições relativas entre ponto e circunferência
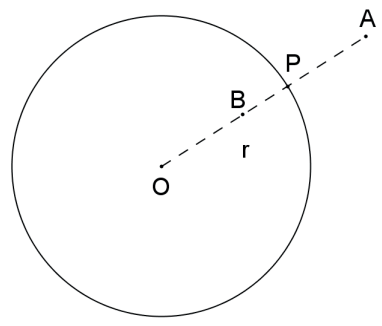
O ponto B pertence ao interior da circunferência de centro O e raio r se, e somente se, a distância desse ponto ao centro da circunferência é menor do que o raio: O̲B̲ < r .
O ponto P pertence à circunferência de centro O e raio r se, e somente se, a distância desse ponto ao centro da circunferência é igual ao raio: O̲P̲ = r.
O ponto A pertence ao exterior da circunferência de centro O e raio r se, e somente se, a distância desse ponto ao centro da circunferência é maior do que o raio: O̲A̲ > r.
Exemplo:
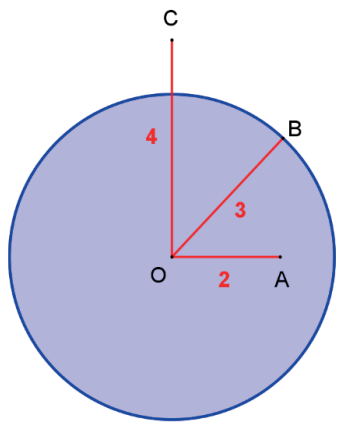
Seja uma circunferência de centro O e raio r=3. Identifique a posição relativa entre os pontos A, B, C e a circunferência, sabendo-se que O̲A̲ = 2 , O̲B̲ = 3 e O̲C̲ = 4.
Resolução:
O ponto A é interior à circunferência, pois O̲A̲ = 2 < 3 = r.
O ponto B pertence à circunferência, pois O̲B̲ = 3 = r.
O ponto C é exterior à circunferência, pois O̲C̲ = 4 > 3 = r.
Veja a figura a seguir, na qual esses pontos estão representados.