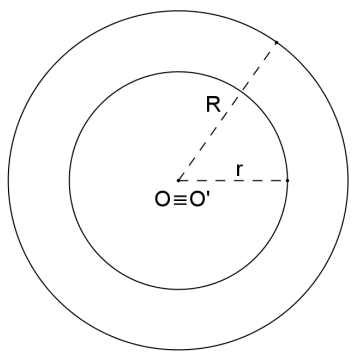
Sejam duas circunferências de centros O e O’, e raios r e R, respectivamente.
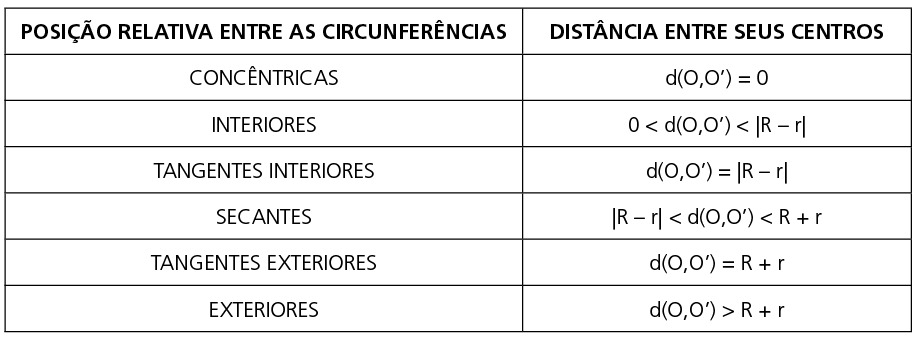
As circunferências são CONCÊNTRICAS se, e somente se, a distâncias entre seus centros é nula: d(O, O’)=0.
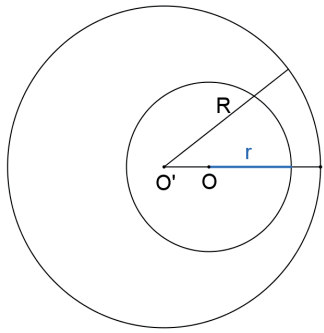
As circunferências são INTERIORES se, e somente se, a distância entre seus centros é maior do que zero e menor do que o módulo da diferença entre seus raios: 0<d(O,O’)<|R – r|.
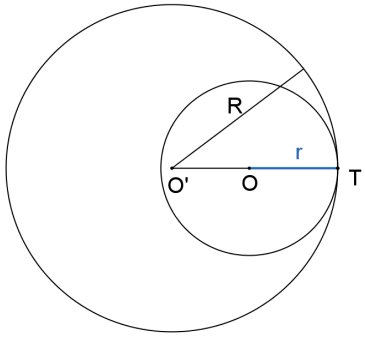
As circunferências são TANGENTES INTERIORES se, e somente se, a distância entre seus centros é igual ao módulo da diferença entre seus raios: d(O,O’)=|R – r|.
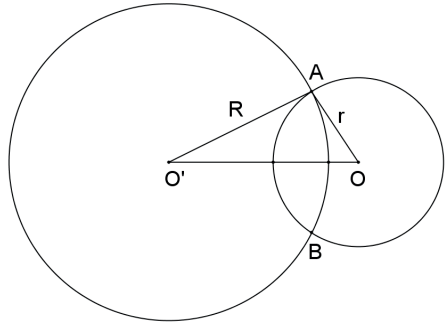
As circunferências são SECANTES se, e somente se, a distância entre seus centros é maior do que o módulo da diferença entre seus raios e menor do que a soma dos raios: |R – r|<d(O,O’)<R+r.
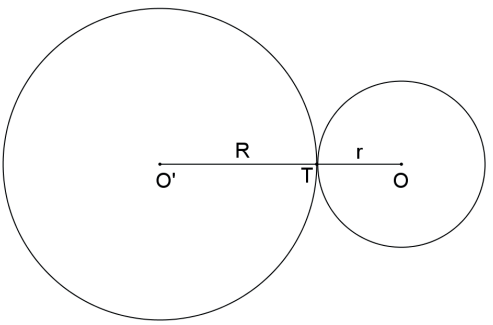
As circunferências são TANGENTES EXTERIORES se, e somente se, a distância entre seus centros é igual à soma dos raios: d(O,O’)=R+r.
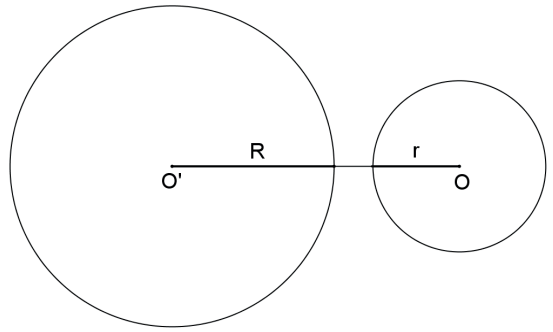
As circunferências são EXTERIORES se, e somente se, a distância entre seus centros é maior do que a soma dos raios: d(O,O’)>R+r.
Exemplo:
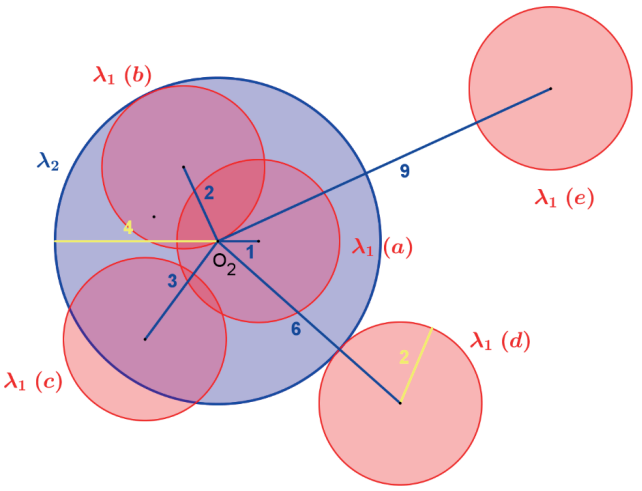
Sejam duas circunferências λ1 e λ2 de raios R1 = 2 e R2 = 4 e centros O1 e O2, respectivamente. Identifique a posição relativa entre as circunferências em cada um dos casos a seguir:

Resolução:
a) As circunferências são interiores, pois O̲1̲O̲2̲ = 1< 2 = R2 – R1.
b) As circunferências são tangentes interiores, pois O̲1̲O̲2̲ = 1 = 2 = R2 – R1.
c) As circunferências são secantes, pois R2-R1= 2 < O̲1̲O̲2̲ = 3 < 6 = R1 + R2.
d) As circunferências são tangentes exteriores, pois O̲1̲O̲2̲ = 6 = R1 + R2.
e) As circunferências são exteriores, pois O̲1̲O̲2̲ = 9 > 6 = R1 + R2.
Veja a figura a seguir onde foi feita uma representação esquemática das cinco situações.