PONTOS NOTÁVEIS DOS TRIÂNGULOS
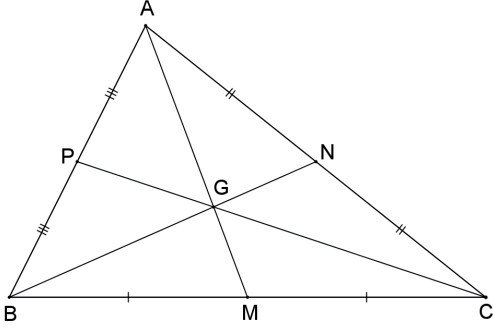
BARICENTRO
As três medianas de um triângulo interceptam-se em um único ponto denominado baricentro. O baricentro divide as medianas na razão 2 : 1, onde a parte maior é a que contém o vértice.
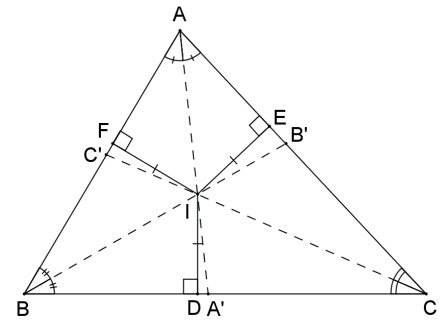
INCENTRO
As três bissetrizes internas de um triângulo interceptam-se em um único ponto denominado incentro e que equidista dos lados do triângulo.
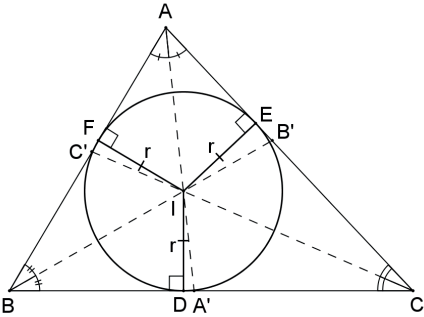
O incentro de um triângulo é o centro da circunferência inscrita no triângulo.
ORTOCENTRO
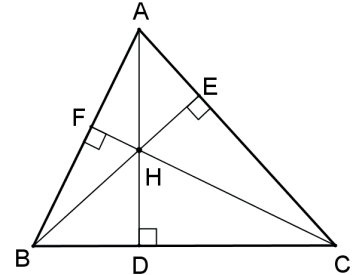
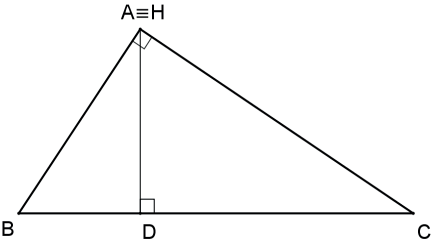
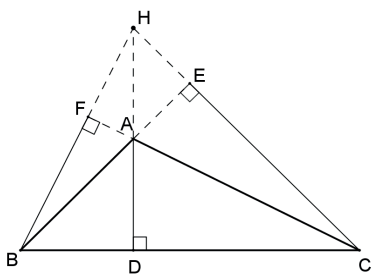
As três alturas de um triângulo (ou seus prolongamentos) concorrem em um único ponto denominado ortocentro.
Nas figuras seguintes, H é o ortocentro dos triângulos.
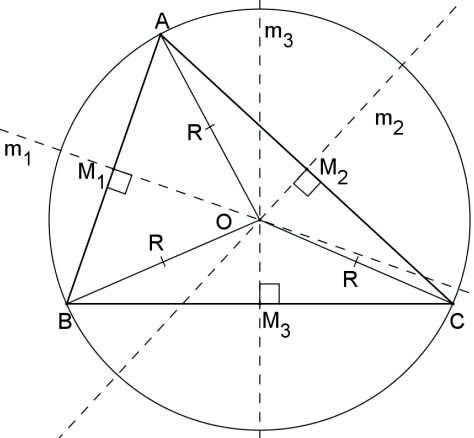
CIRCUNCENTRO
As mediatrizes dos lados de um triângulo interceptam-se em um único ponto denominado circuncentro e que equidista dos vértices do triângulo.
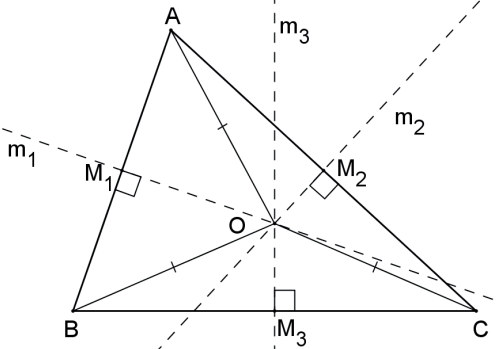
O circuncentro de um triângulo é o centro da circunferência circunscrita ao triângulo.