Geometria Plana: Polígonos Regulares

POLÍGONOS REGULARES

Um polígono regular é um polígono equilátero e equiângulo.

Os polígonos regulares são inscritíveis e circunscritíveis. O centro das circunferências inscrita e circunscrita é chamado centro do polígono.

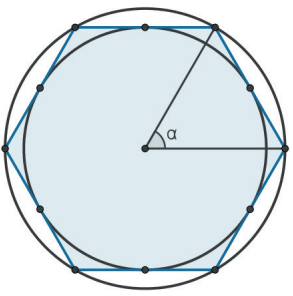
Cada ângulo interno de um polígono regular é igual a Â_i = ^Si/_n = ^180°(n−2)/_n e cada ângulo externo é igual a Â_e = ^Se/_n = ^360°/_n.

ÂNGULO CENTRAL

Imagine o triângulo formado pelos raios da circunferência circunscrita ao polígono regular e um dos lados do polígono, como na figura abaixo.

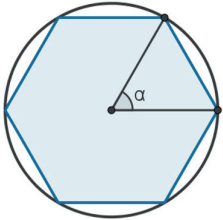
O ângulo central αα é o ângulo do vértice do triângulo que coincide com o centro do polígono.

O ângulo central de um polígono regular é igual a ÂC = ^360°/_n.

APÓTEMA DE UM POLÍGONO

O apótema de um polígono regular é a distância do centro do polígono a qualquer um dos lados.

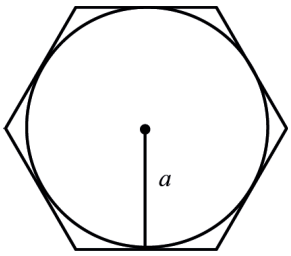
Dessa forma, podemos perceber que sempre que traçamos o apótema temas o triângulo abaixo formado.

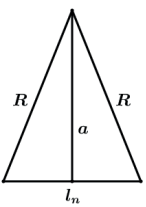
Dessa forma por termos sempre um triângulo isósceles, teremos que

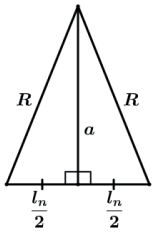
E assim sendo, o apótema a de qualquer polígono regular é perpendicular ao lado do polígono dividindo-o ao meio.

DIAGONAIS QUE PASSAM PELO CENTRO

Um polígono regular de gênero n par possui d_c = ⁿ/₂ diagonais que passam pelo centro e d_nc = ⁿ⁽ⁿ⁻⁴⁾/₂ diagonais que não passam pelo centro.

Um polígono regular de gênero ímpar não possui diagonais que passam pelo centro.