Geometria Plana: Losango, Trapézio e polígono regular

Losango, trapézio e polígono regular são figuras geométricas. O losango possui lados iguais, o trapézio tem pelo menos um par de lados paralelos e os polígonos regulares têm todos os lados e ângulos congruentes. Essas figuras desempenham papéis essenciais na geometria.

LOSANGO

A área do losango é igual à metade do produto de suas diagonais.

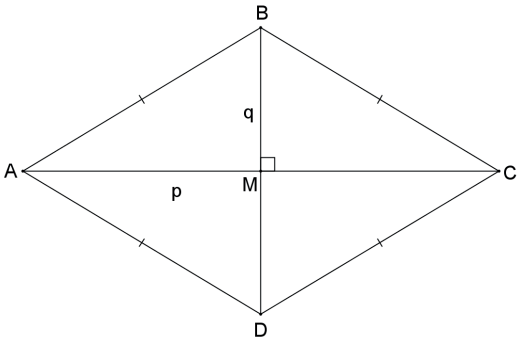
Seja o losango ABCD de diagonais AC = p e BD = q, então sua área é S_ABCD = ^p⋅q/₂.

Demonstração:

Inicialmente, cabe observar que o losango possui diagonais perpendiculares.

Assim:

TRAPÉZIO

A área do trapézio é igual ao produto da semissoma de suas bases pela sua altura.

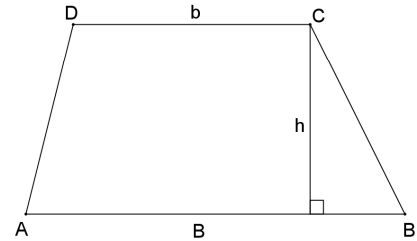
Seja o trapézio ABCD de bases AB = B e CD = b, e altura h, então sua área é S = ^B+b/₂⋅ h.

Demonstração:

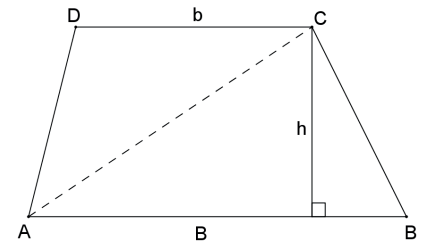
POLÍGONO REGULAR

A área de um polígono regular é igual ao produto do semiperímetro pelo apótema.

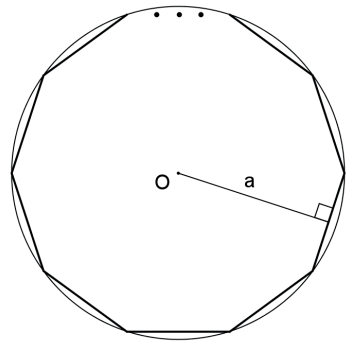
Seja um polígono regular de semiperímetro p e apótema a, então sua área é S = p ⋅ a.