CONCEITOS INICIAIS
NOÇÕES AXIOMÁTICAS
Alguns elementos geométricos são tão primitivos que dispensam qualquer definição, dentre eles estão o ponto.
O PONTO
O ponto é representado por uma letra maiúscula do nosso alfabeto.
A RETA
A reta é a reunião de infinitos pontos alinhados, é um elemento que não possui largura apenas comprimento. A reta é representada por uma letra minúscula do nosso alfabeto ou ainda com símbolos que veremos a frente.
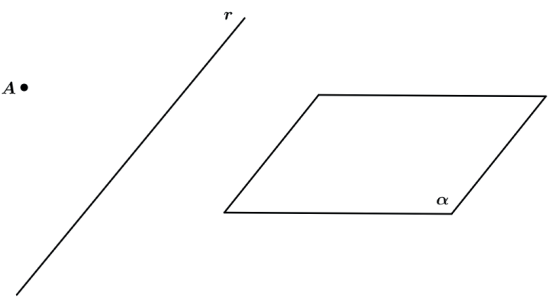
O PLANO
É compreendido como uma superfície plana que não faz curva. Planos são figuras geométricas bidimensionais formadas pela reunião de infinitas retas, perpendiculares a uma reta dada, dispostas lado a lado.
POSTULADOS PRINCIPAIS
- Dois pontos distintos determinam uma única reta que passa por eles.
- Pontos colineares são pontos que pertencem a uma mesma reta.
- Três pontos não colineares determinam um único plano que passa por eles.
- Por um ponto não pertencente a uma reta, passa uma, e apenas uma, reta paralela à primeira (Euclides).
POSIÇÕES RELATIVAS
ENTRE PONTOS
a) Coincidentes
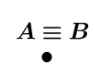
b) Distintos

ENTRE RETAS
a) Concorrentes: um ponto de interseção
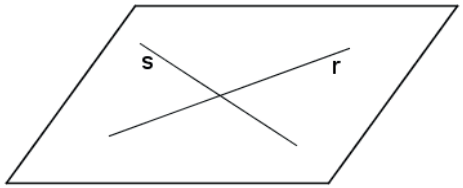
b) Paralelas Coincidentes: infinitos pontos de interseção
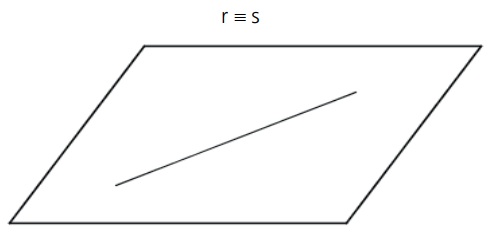
c) Paralelas Paralelas: não há pontos de interseção
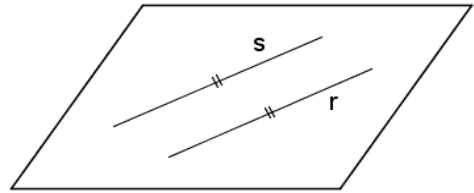
Retas paralelas são retas coincidentes ou são retas coplanares que não possuem ponto em comum.
- Se duas retas são paralelas a uma terceira, então elas são paralelas entre si.
DEFINIÇÕES E REPRESENTAÇÕES
- Reta
A reta é um elemento infinito e dessa forma sua representação é mais complexa a partir somente de um desenho então pelo próprio postulado de determinação da reta, tendo conhecido 2 pontos A e B que pertencem a uma reta podemos representar uma reta por AB↔.

- Semirreta
Podemos entender como um elemento que possui início mas não possui fim, pode-se entender também como a reta com um de seus lados tendo sido “cortado”, assim podemos ter a semirreta de início em A e na direção de B (AB→) ou a semirreta de início em B e na direção de A (AB).

- Segmento de Reta
O segmento de reta possui início e fim e dessa forma é o único mensurável, que se pode medir. É simbolizado pelos pontos dos seus extremos (A̲B̲).

CLASSIFICAÇÕES DOS SEGMENTOS
- Consecutivos
São os segmentos que onde termina o primeiro o seguinte imediatamente continua.
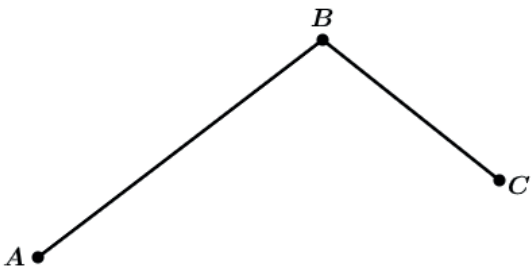
- Colineares
São segmentos que estão alinhados, ou seja, sobre a mesma reta.

A̲B̲ e C̲D̲ são colineares e ambos estão sobre a reta r.
- Consecutivos
São os segmentos ao mesmo tempo consecutivos e colineares

PERPENDICULARIDADE
Retas perpendiculares (⊥) são retas concorrentes que formam ângulos adjacentes suplementares congruentes.
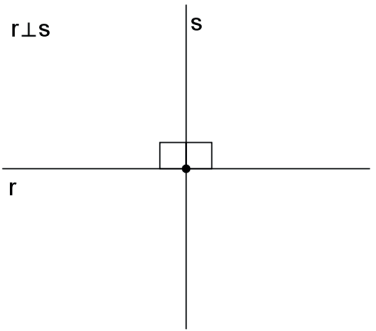
- Num plano, por um ponto dado de uma reta, passa uma única reta perpendicular à reta dada.
- A projeção ortogonal de um ponto sobre uma reta é o ponto de interseção da reta com a perpendicular a ela passando pelo ponto dado.
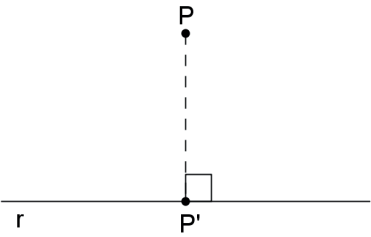
Na figura acima, o ponto P’ é a projeção ortogonal do ponto P sobre a reta r.
- A projeção ortogonal de um segmento de reta não perpendicular a uma reta sobre ela, é o segmento determinado sobre a reta pelas projeções dos extremos do segmento original.
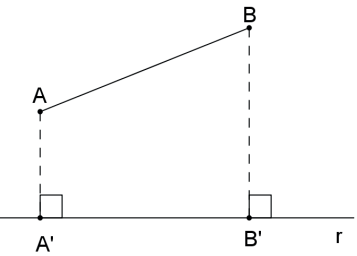
Na figura acima, o segmento A̲’B̲’ é a projeção ortogonal do segmento de reta A̲B̲ sobre a reta r.
DISTÂNCIAS
- A distância entre dois pontos A e B é a medida do segmento de reta AB.
- A distância entre um ponto e uma reta é distância do ponto ao pé da perpendicular à reta conduzida pelo ponto.
- A distância entre duas retas paralelas é distância entre um ponto qualquer de uma das retas e a outra reta.




