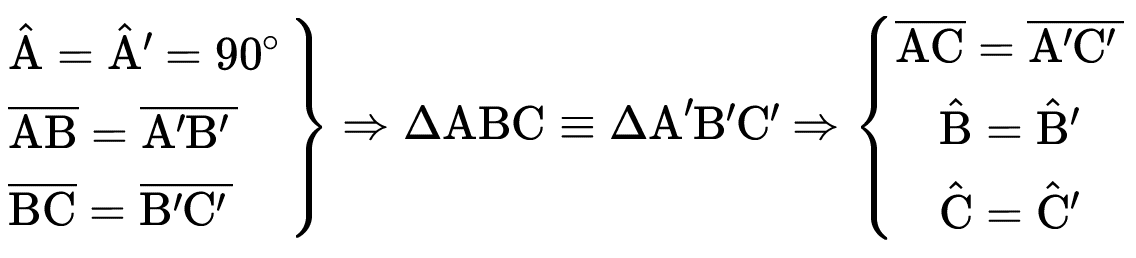DESIGUALDADES NO TRIÂNGULO
RELAÇÃO ENTRE LADOS E ÂNGULOS
Teorema: Num triângulo qualquer, ao maior (menor) lado, opõe-se o maior (menor) ângulo. Mais precisamente, em um ∆ABC, tem-se  > B^ se, e somente se, BC > AC
Demonstração:
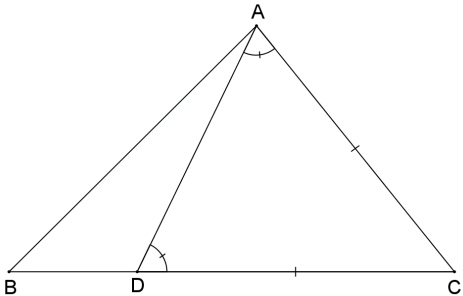
(Volta) Seja BC > AC, então marquemos no segmento B̲C̲, um ponto D tal que C̲D̲ = A̲C̲. O triângulo ADC é isósceles, portanto  >DÂC = AD^C > B^.
(Ida) Seja  > B^. Não podemos ter BC = AC, pois se teria  = B^. Também não podemos ter BC < AC, pois a demonstração anterior implicaria  < B^. Portanto, a única possibilidade é BC > AC.
DESIGUALDADE TRIANGULAR
Teorema: Cada lado de um triângulo é menor que a soma dos outros dois.
Logo, em um triângulo ABC, de lados a, b e c, temos:
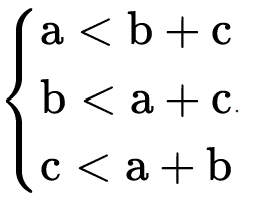
Demonstração:
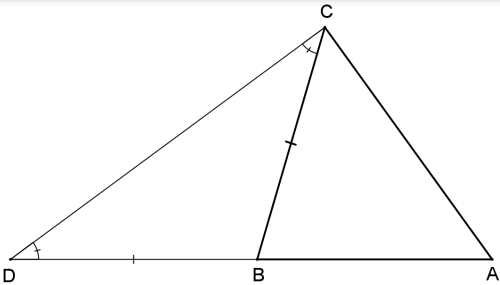
Tomemos um ponto D na reta AB de forma que B está entre A e D e que BD = BC. Como o ∆ DBC é isósceles, temos AD^C = BD^C = BC^D < AC^D.
Aplicando a desigualdade (1.1) ao ∆ADC, tem-se AC<AD=AB+BD=AB+BC, como queríamos demonstrar.
ProBizu: A condição pode ser garantida também, quando o maior lado é conhecido, verificando-se apenas que o maior lado é menor que a soma dos outros dois lados.
Alternativamente, quando o menor lado é conhecido, podese verificar apenas que o menor lado é maior que o módulo da diferença dos outros dois lados.
Corolário: A menor distância entre dois pontos é o segmento de reta que os une.
Exemplo: Sejam os pontos A e B do mesmo lado de uma reta r. Identifique o ponto C ∈ r tal que AC + CB assume o valor mínimo.
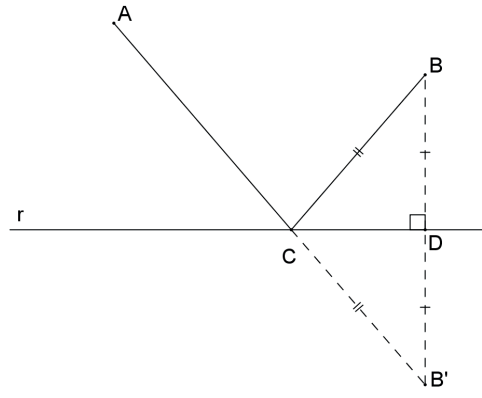
Seja B’ a reflexão do ponto B em relação à reta r, então BC = B’C. O menor caminho de A a B’ é o segmento de reta que une esses dois pontos. Como AC + CB = AC + CB’, então o ponto C que faz AC + CB assumir o valor mínimo é a interseção do segmento AB’ com a reta r.
ENVOLVENTE E ENVOLVIDA
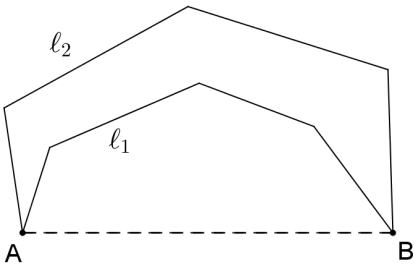
Teorema: Dadas duas curvas convexas que unem dois pontos distintos, sendo uma envolvente e a outra envolvida, a envolvente é maior que a envolvida.
Sejam ℓ1 e ℓ2 os comprimentos das duas curvas convexas indicadas na figura, então ℓ2 > ℓ1.
CONGRUÊNCIA DE TRIÂNGULOS
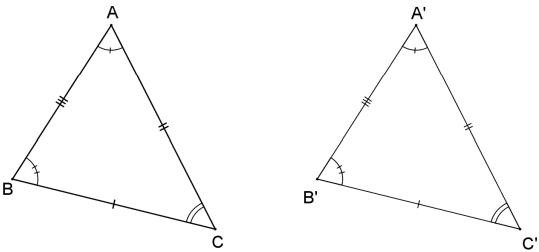
Dois triângulos são ditos congruentes (símbolo ≡) se, e somente se, é possível estabelecer uma correspondência entre seus vértices de modo que: seus lados são ordenadamente congruentes e seus ângulos são ordenadamente congruentes.
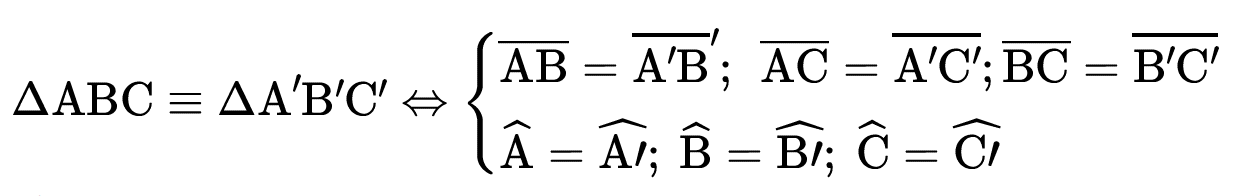
CRITÉRIOS DE CONGRUÊNCIA DE TRIÂNGULOS
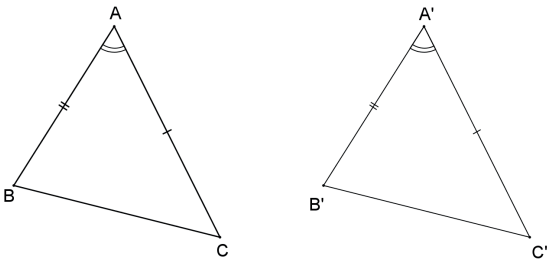
Critério Lado – Ângulo – Lado (L.A.L.)
Se dois lados de um triângulo e o ângulo por eles formado forem congruentes a dois lados de outro triângulo e ao ângulo por eles formados, respectivamente, então esses dois triângulos são congruentes (postulado).
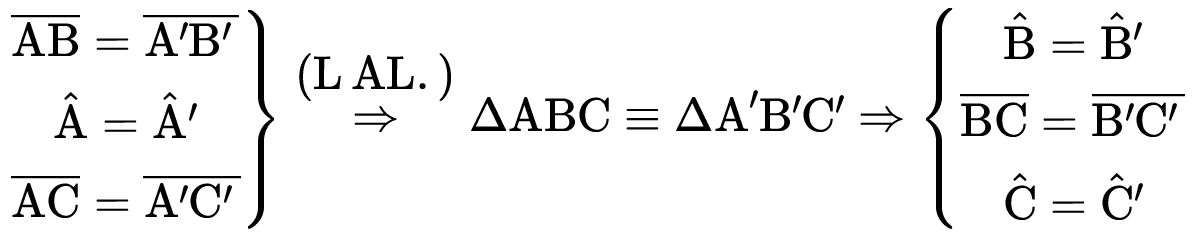
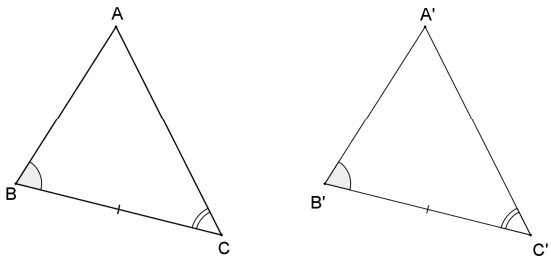
Critério Ângulo – Lado – Ângulo (A.L.A.)
Se um dos lados de um triângulo e os ângulos adjacentes a esse lado forem congruentes a um dos lados de outro triângulo e aos ângulos adjacentes a esse lado, respectivamente, então esses dois triângulos são congruentes (teorema).
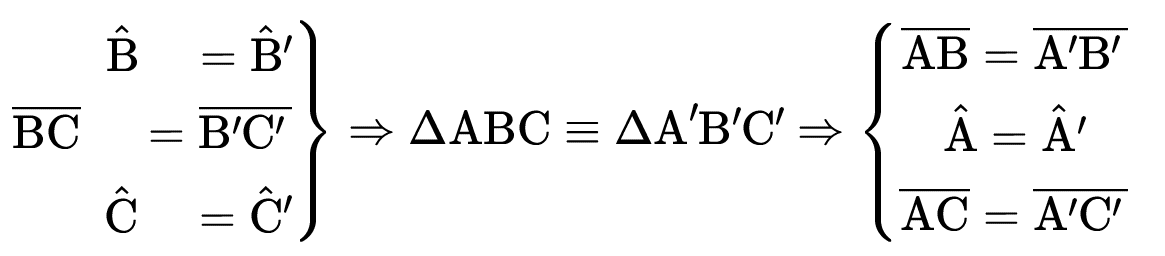
Critério Lado – Lado – Lado (L.L.L.)
Se os três lados de um triângulo são respectivamente congruentes aos três lados de outro triângulo, então esses dois triângulos são congruentes (teorema).
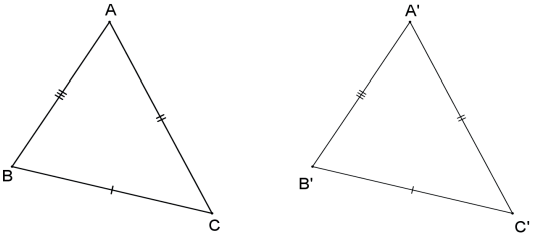

Critério Lado – Ângulo – Ângulo oposto (L. A. Ao.)
Se um lado, um ângulo adjacente e o ângulo oposto a esse lado, de dois triângulos são ordenadamente congruentes, então esses dois triângulos são congruentes.
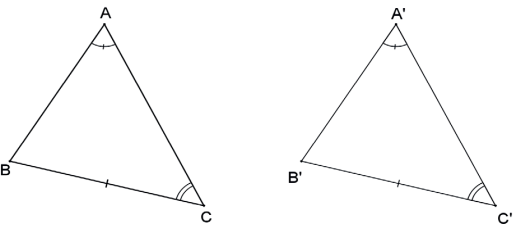
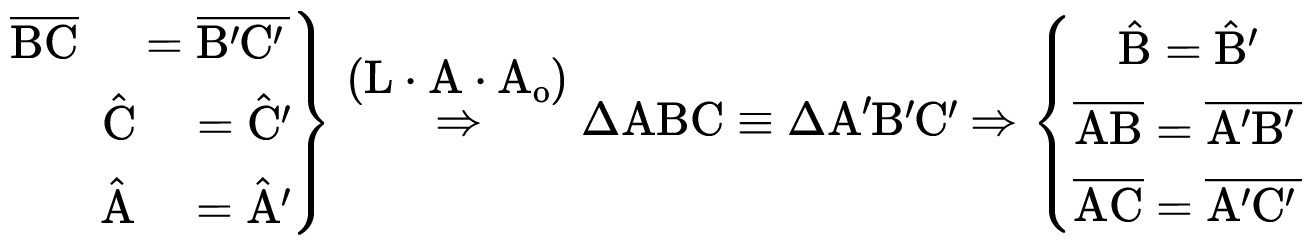
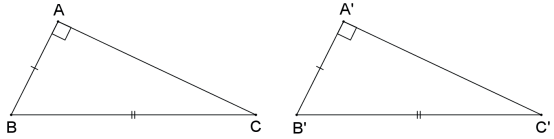
CRITÉRIO ESPECIAL DE CONGRUÊNCIA DE TRIÂNGULOS RETÂNGULOS
Se dois triângulos retângulos têm um cateto e a hipotenusa, respectivamente, congruentes, então esses dois triângulos são congruentes.