DEFINIÇÃO
Seja uma sequência de pontos distintos A1, A2, A3′,…,AN, com n ≥ 3, onde três pontos consecutivos não são colineares (AN−1, AN, A1 e An, A1, A2 são considerados consecutivos). A reunião dos segmentos A̲1̲A̲2̲, A̲2̲A̲3̲, …, A̲n−1A̲n, A̲nA̲1 é o polígono A1A2 … AN.
Os pontos A1,A2,A3,…,An são os vértices do polígono; os segmentos A̲1̲A̲2̲, A̲2̲A̲3̲, …, A̲n−1A̲n, A̲n1A̲n são os seus lados; e os ângulos Â1 = AnÂ1A2, Â2 = A1Â2A3,…, Ân = An−1ÂnA1 são os ângulos internos do polígono.
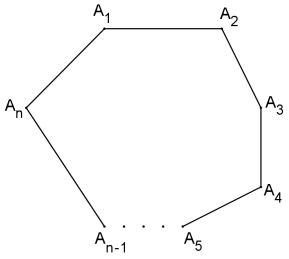
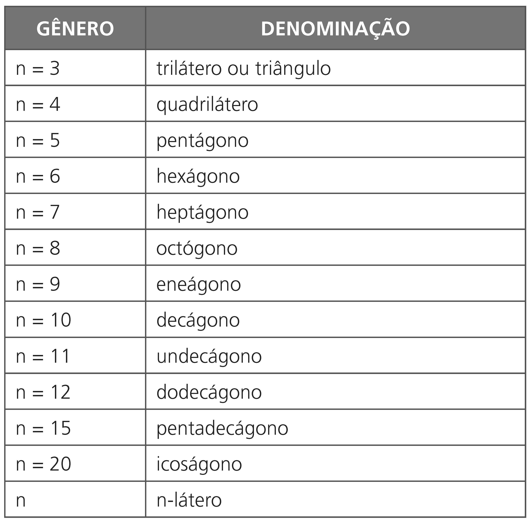
Um polígono de n vértices possui também n lados e n ângulos, e diz-se de gênero n.
Um polígono é simples se, e somente se, a interseção de quaisquer dois lados não consecutivos é vazia.
Um polígono simples é convexo se, e somente se, a reta determinada por quaisquer dois de seus vértices consecutivos deixa todos os outros vértices no mesmo semiplano.
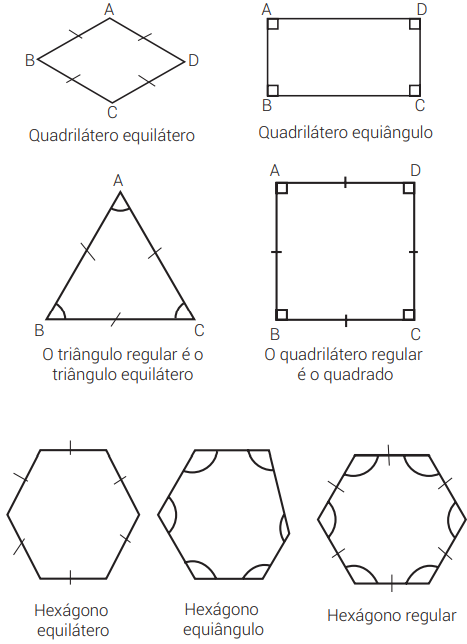
Um polígono que possui todos os lados congruentes é dito equilátero. Um polígono que possui todos os ângulos congruentes é dito equiângulo. Um polígono é dito regular se é equilátero e equiângulo.
O desenvolvimento a seguir refere-se a polígonos simples que possuem todos os vértices no mesmo plano.
ÂNGULOS INTERNOS
A soma dos ângulos internos de um polígono de gênero n é:
Si = 180°(n−2)
Demonstração:
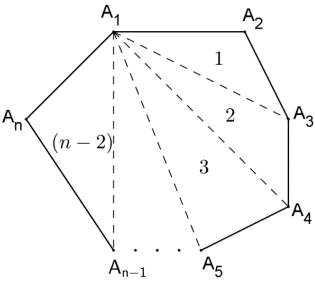
Ligando-se um dos vértices de um polígono gênero n aos (n−3) vértices não adjacentes a ele, o polígono fica dividido em (n−2) triângulos. A soma dos ângulos internos desses (n−2) triângulos é igual à soma dos ângulos internos do polígono. Assim, a soma dos ângulos internos do polígono é Si = 180°(n−2).
ÂNGULOS EXTERNOS
Ângulo externo de um polígono é o ângulo suplementar adjacente do ângulo interno do polígono.
A soma dos ângulos externos de um polígono de gênero n é:
Se = 360°
Demonstração:
Há n pares de ângulos internos e externos, e cada par soma 180º. Assim, a soma de todos os ângulos internos e externos do polígono é 180º·n. Portanto,
Si + Se = 180°⋅n ⇔ 180e(n−2) + Se = 180°n ⇔ Se = 360°
Observe que a soma dos ângulos externos de um polígono é constante e não depende de seu gênero.




