Geometria Plana: Bissetrizes internas e externas

BISSETRIZES INTERNAS

Seja um triângulo ABC de lados B̲C̲ = a, A̲C̲ = b e A̲B̲ = c, semiperímetro p, e bissetrizes internas A̲D̲ = β_iA, B̲E̲ = β_iB e C̲F̲ = β_iC relativas aos lados B̲C̲, A̲C̲ e  A̲B̲, respectivamente, então

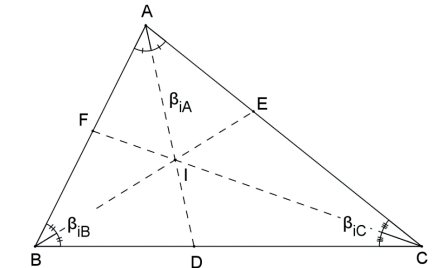
Demonstração:

Sejam BD = m e CD = n. 

Aplicando o teorema das bissetrizes internas no ∆ ABC, temos:

Aplicando a relação de Stewart, temos: c²n + b²m = x²a + amn. Desenvolvendo as 2 equações teremos: (β_iA)² = bc – mn.

Analogamente, prova-se que (β_iA)² = B̲C̲ · A̲B̲ – C̲E̲ · A̲E̲ e (βiC)2 = A̲C̲ · C̲B̲ – A̲F̲ · B̲F̲.

Exemplo:

No triângulo ABC, o ponto D do lado BC é tal que AD é bissetriz do ângulo BAC. Se AB = 2, AD = 3 e AC = 6, o lado BC mede:

a) 3
b) 4
c) 5
d) √10
e) √12

Resolução: B

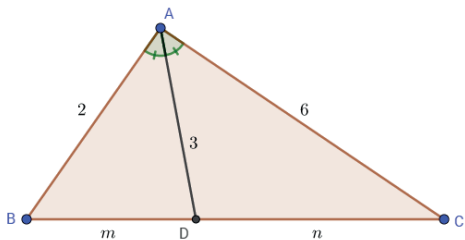
Utilizando a fórmula β² = bc – mn e o teorema da bissetriz interna ²/_m = ⁶/_n ⇒ n = 3m temos:

3² = 2 · 6 – m · 3m ⇒ -3m2 = -3 ⇒ m = 1 ⇒ n= 3m =3 ⇒ a = m + n = 4

BISSETRIZES EXTERNAS

Seja um triângulo ABC de lados B̲C̲ = a, A̲C̲ = b e A̲B̲ = c, semiperímetro p, e bissetrizes externas β_eA, β_eB e β_eC relativas aos lados B̲C̲, A̲C̲ e A̲B̲, respectivamente, então

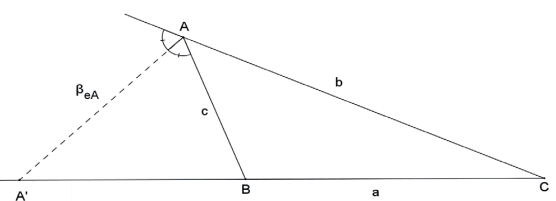
Demonstração:

A demonstração é análoga à das bissetrizes internas. Deve-se aplicar o teorema das bissetrizes externas para encontrar o ponto A’ e, posteriormente, a relação de Stewart para encontrar AA’.