Ângulo é a reunião de duas semirretas de mesma origem.
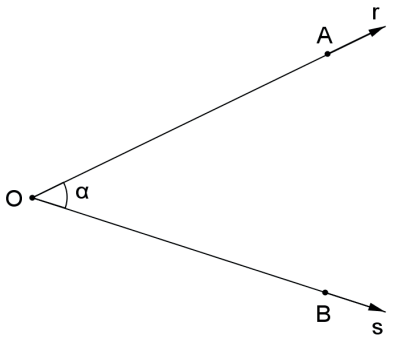
Notações: AÔB; OA OB; Ô; α.
O ponto O é o vértice do ângulo e as semirretas OA→ e OB→ são os lados do ângulo.
Um ângulo determina dois setores angulares, um convexo e outro côncavo, exceto no caso de semirretas opostas.
BISSETRIZ DE UM ÂNGULO
A bissetriz de um ângulo é uma semirreta que o divide em dois ângulos congruentes.
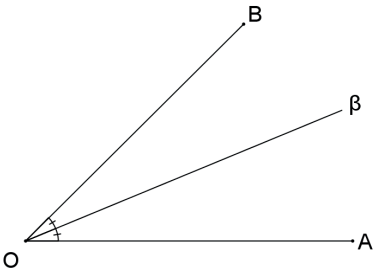
ProBizu: A bissetriz de um ângulo é o lugar geométrico dos pontos que equidistam dos lados de um ângulo.
ÂNGULOS OPOSTOS PELO VÉRTICE
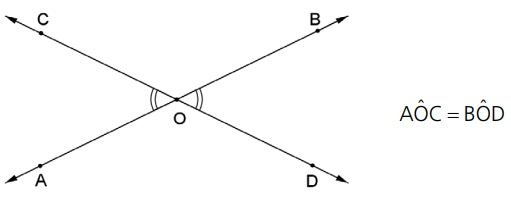
Dois ângulos são opostos pelo vértice (o.p.v.) se, e somente se, os lados de um deles são as respectivas semirretas opostas aos lados do outro.
Dois ângulos opostos pelo vértice são congruentes.
- Duas retas concorrentes determinam dois pares de ângulos opostos pelo vértice.
- As bissetrizes de dois ângulos opostos pelo vértice são semirretas opostas.
ÂNGULOS CONSECUTIVOS
Dois ângulos são consecutivos se, e somente se, possuem um lado em comum.
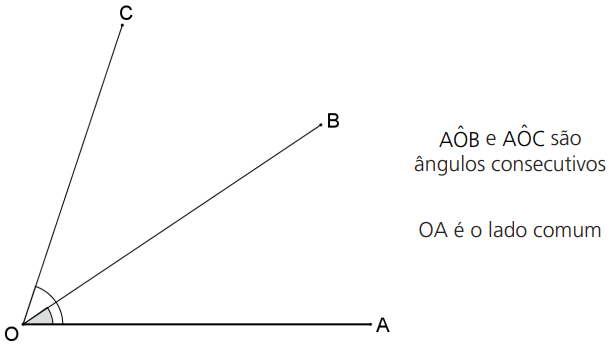
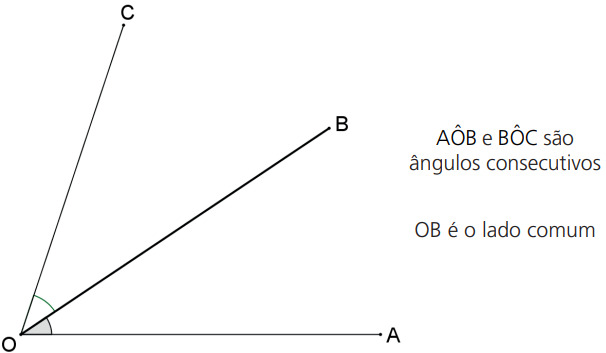
ÂNGULOS ADJACENTES
Dois ângulos são adjacentes se, e somente se, são consecutivos e não possuem pontos internos comuns.
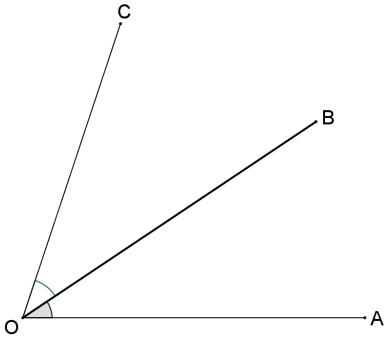
Os ângulos AÔB e BÔC , que possuem lado comum OB, são ângulos adjacentes.
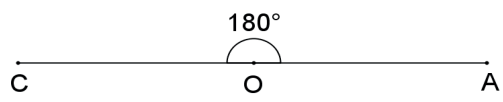
ÂNGULO RASO
Ângulo raso é o ângulo determinado por duas semirretas opostas. Um ângulo raso mede 180º.
ÂNGULO SUPLEMENTAR ADJACENTE
Dado o ângulo AÔB, o ângulo suplementar adjacente de AÔB é o ângulo determinado pelas semirretas OB→ e OC→, semirreta oposta à semirreta OA→, ou seja, determinado por um dos lados do ângulo e pela semirreta oposta ao outro lado.
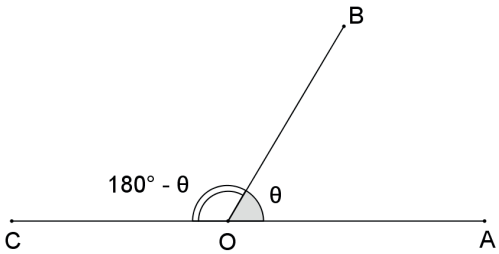
A medida do ângulo suplementar adjacente de é 180º – θ.
ÂNGULO RETO
Ângulo reto é aquele que é igual a seu suplementar adjacente. A medida de um ângulo reto é 90º.
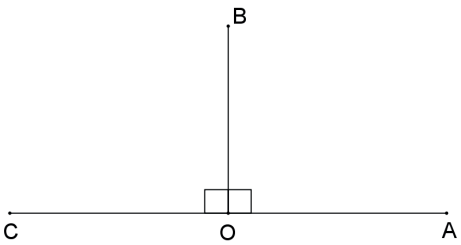
De fato, se θ é um ângulo reto, temos: θ = 180º – θ ⇔ θ = 90º.
ÂNGULO AGUDO E ÂNGULO OBTUSO
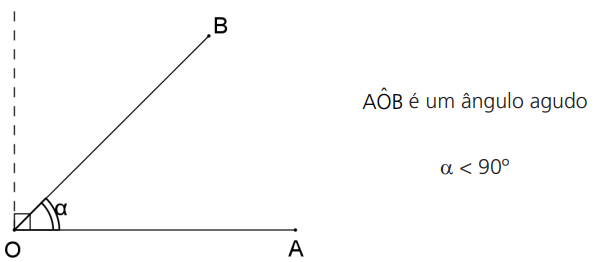
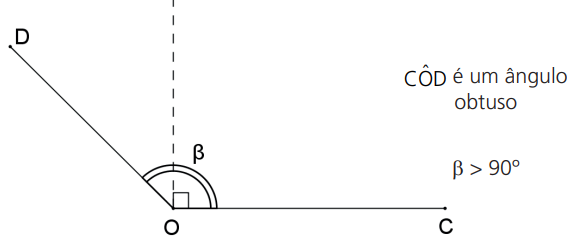
Ângulo agudo é aquele que é menor que um ângulo reto e ângulo obtuso é aquele que é maior que um ângulo reto.
UNIDADES DE MEDIDAS ANGULARES
- SISTEMA SEXAGESIMAL − GRAU (°)
Um sistema sexagesimal é um sistema de numeração de base 60, ou seja, cada submúltiplo é 60 vezes menor que o anterior.
Para medidas angulares, é comum adotar um sistema sexagesimal com unidade de medida 1 grau (1º) que é 1/90 de um ângulo reto.
Um grau pode ser dividido em 60 minutos e cada minuto dividido em 60 segundos.
1° = 1/90 ⋅ (ângulo reto) ⇔ 1 ângulo reto = 90°
1 ângulo raso = 180°
1 ângulo de uma volta = 360°
Submúltiplos do grau:
Minuto: 1′= 1/60 ⋅1° ⇔ 1°= 60′
Segundo: 1′′= 1/60 ⋅ 1′ ⇔ 1′= 60′′ ⇔ 1°= 3600′′
- SISTEMA DECIMAL − GRADO (gr)
Um sistema decimal é um sistema numeração de base 10, ou seja, cada submúltiplo é 10 vezes menor que o anterior.
Para medidas angulares, utiliza-se um sistema decimal com unidade de medida 1 grado (1 gr), que equivale a 1/100 de um ângulo reto.
1gr = 1/100 ⋅ (ângulo reto) ⇔ 1 ângulo reto = 100gr
1 ângulo raso =200gr
1 ângulo de uma volta =400gr
- SISTEMA CIRCULAR OU RADIOMÉTRICO − RADIANOS (rad)
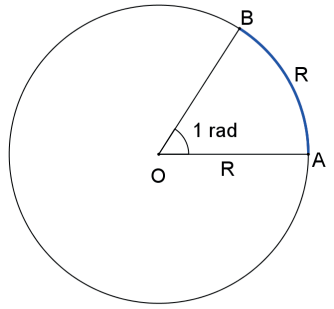
O ângulo de 1 radiano (1 rad) é o ângulo central em uma circunferência de raio R que determina um arco de comprimento R sobre essa circunferência.
O sistema circular ou radiométrico adota como unidade de medida 1 radiano (1 rad).
Como o comprimento de uma circunferência de raio R é 2πR, então um ângulo de uma volta mede 2π rad.

- RELAÇÕES ENTRE AS UNIDADES
180º = 200 gr = π rad
- NÚMERO COMPLEXO
Número complexo é um número que apresenta mais de uma unidade de um mesmo sistema para exprimir uma grandeza.
Exemplos: 2h 30 min 10 seg e 15°20’32”.
Número incomplexo é um número que apresenta uma única unidade de um sistema para exprimir uma grandeza.
Exemplos: 135,2 min e 65,32°.
ÂNGULOS COMPLEMENTARES
Ângulos complementares são ângulos cujas medidas somam um ângulo reto (90º).
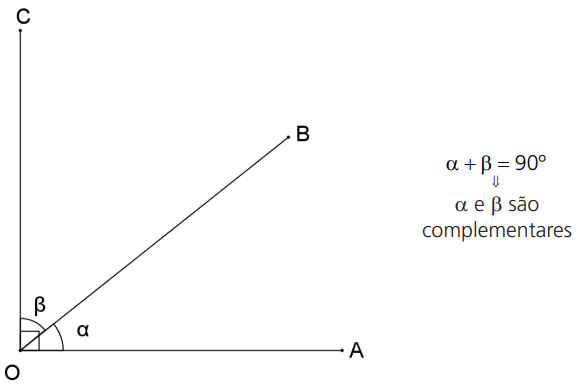
O complemento de um ângulo é o ângulo que, junto ao primeiro, forma um par de ângulos complementares. Portanto, o complemento de x é 90º – x.
Complemento de x = 90º – x
ÂNGULOS SUPLEMENTARES
Ângulos suplementares são ângulos cujas medidas somam um ângulo raso (180º).
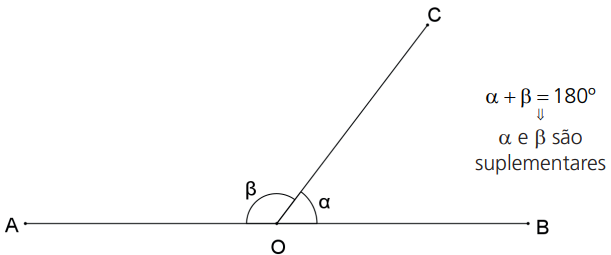
O suplemento de um ângulo é o ângulo que, junto ao primeiro, forma um par de ângulos suplementares. Portanto, o suplemento de x é 180º – x.
Suplemento de x = 180º – x
As bissetrizes de dois ângulos adjacentes suplementares são perpendiculares.
ÂNGULOS REPLEMENTARES
Ângulos replementares são ângulos cujas medidas somam um ângulo de uma volta (360°).
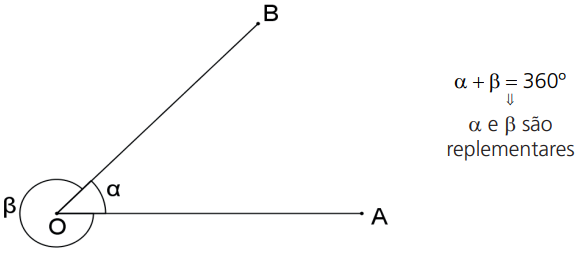
O replemento de um ângulo é o ângulo que, junto ao primeiro, forma um par de ângulos replementares. Portanto, o replemento de x é 360º-x.
ProBizu:
Complemento de x = 90º – x
Suplemento de x = 180º – x
Replemento de x= 360º – x
Observações:
Vamos analisar o problema de identificar o ângulo θ entre os ponteiros das horas e dos minutos de um relógio às H horas e M minutos.
O ângulo entre as marcações de horas é 360°/12 = 30° e o ângulo entre as marcações de minutos é 360°/60 =6°.
A velocidade angular do ponteiro das horas é 30°/60min = 0,5° / min e a velocidade angular do ponteiro dos minutos é 360°/60min = 6° / min.
Às H horas em ponto, o ângulo entre os ponteiros do relógio é AÔB = 30° ⋅ H.
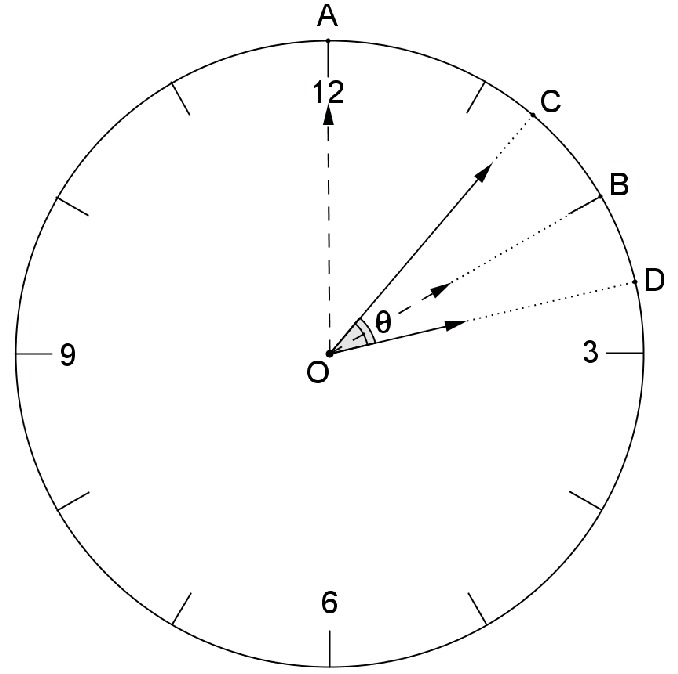
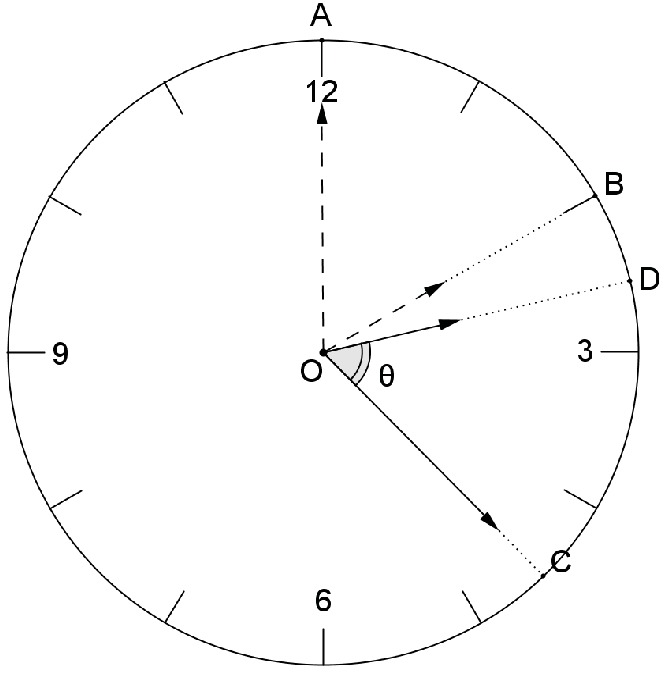
Entre H horas em ponto e H horas e M minutos, passaram-se M minutos. Nesse período, o ponteiro das horas deslocou-se BÔD = 0,5° / min ⋅ Mmin = 0,5° ⋅ M e o ponteiro dos minutos deslocou-se AÔC = 6° / min ⋅ Mmin = 6° ⋅ M. Assim, há duas possibilidades para o ângulo entre os ponteiros das horas e dos minutos:
1º. Se o ponteiro dos minutos não ultrapassou o ponteiro das horas (Figura 1), temos:
θ = CÔD = AÔB + BÔD − AÔC = 30° ⋅ H + 0,5 ⋅ M − 6° ⋅ M = 30e ⋅ H − 5,5° ⋅ M
2°. Se o ponteiro dos minutos ultrapassou o ponteiro das horas (Figura 2), temos:
θ = CÔD = AÔC − AÔB −BÔD = 6° ⋅ M − 30° ⋅ H − 0,5 ⋅ M = 5,5° ⋅ M − 30° ⋅ H
A expressão para o ângulo entre os ponteiros das horas e dos minutos de um relógio às H horas e M minutos pode ser representada de maneira única como:

ProBizu: O ângulo entre os ponteiros de um relógio às H horas e M minutos é:





