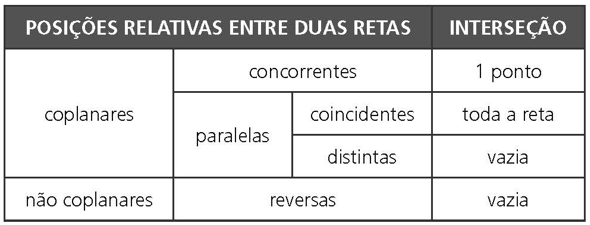
OSIÇÕES RELATIVAS ENTRE RETAS
RETAS COPLANARES
A. Concorrentes: um ponto de interseção.
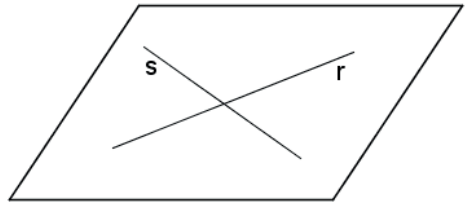
B. Paralelas Coincidentes: infinitos pontos de interseção.
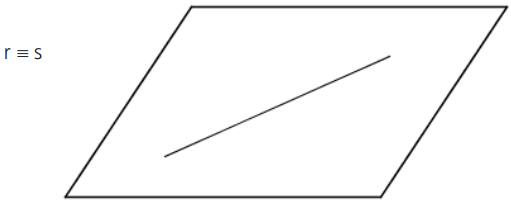
C. Paralelas Distintas: não há pontos de interseção.
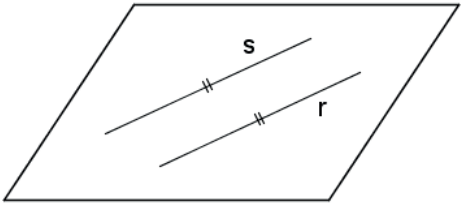
RETAS NÃO COPLANARES
RETAS REVERSAS: não há pontos de interseção.
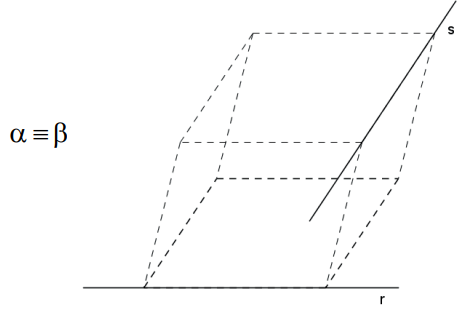
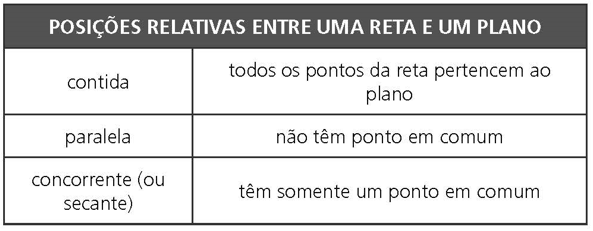
POSIÇÕES RELATIVAS ENTRE RETA E PLANO
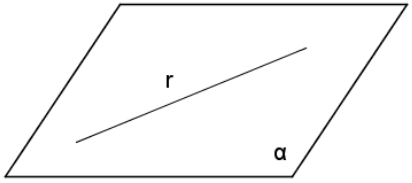
A. Reta e plano contidos: infinitos pontos de interseção.
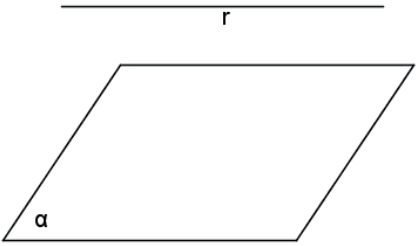
B. Reta e plano paralelos: não há pontos de interseção.
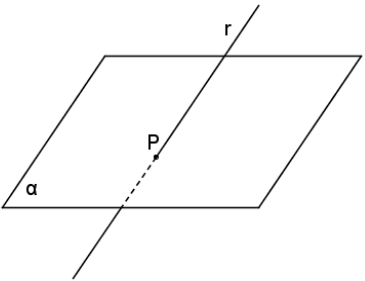
C. Reta e plano secantes: um único ponto de interseção.
POSIÇÕES RELATIVAS ENTRE PLANOS
POSIÇÕES RELATIVAS ENTRE DOIS PLANOS
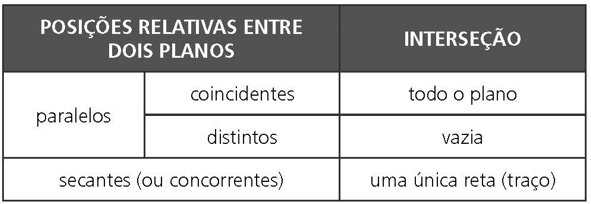
A. Planos paralelos coincidentes: a interseção é todo o plano.
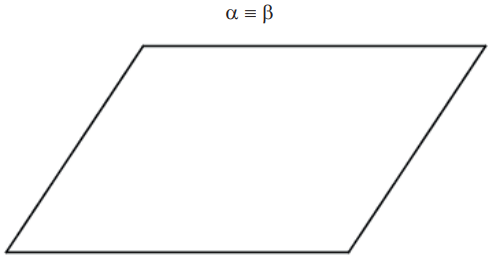
B. Planos paralelos distintos: não há pontos de interseção.
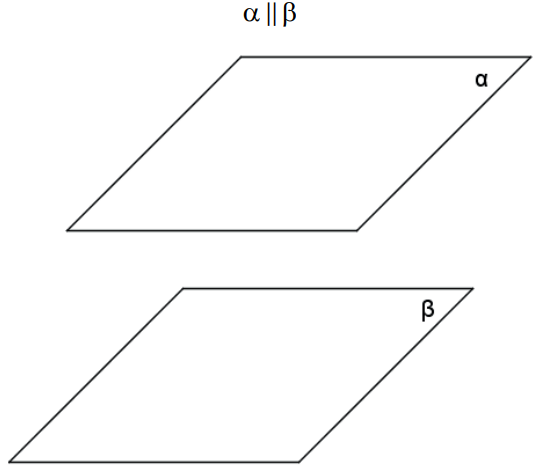
C. Planos secantes (ou concorrentes): a interseção é uma reta.
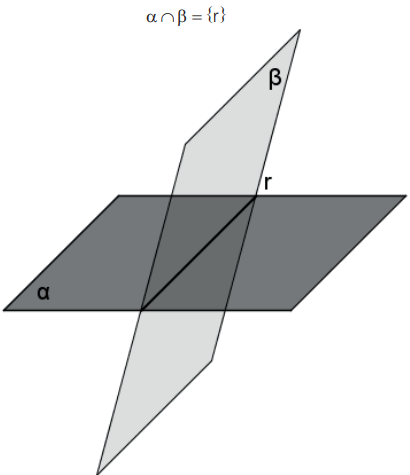
PARALELISMO
- Se duas retas são paralelas a uma terceira, então elas são paralelas entre si.
- Uma reta é paralela a um plano se, e somente se, eles não têm ponto em comum.
TEOREMA: a condição necessária e suficiente para que uma reta não contida em um plano seja paralela a esse plano é que ela seja paralela a uma reta do plano.
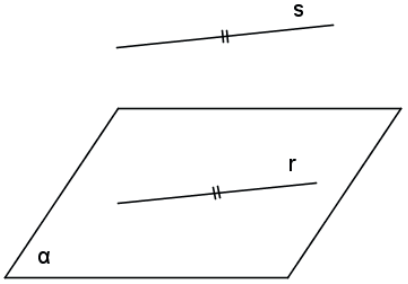
Dois planos são paralelos se, e somente se, não têm ponto em comum ou são coincidentes.
- Por um ponto fora de um plano passa um único plano paralelo a esse plano.
TEOREMA: a condição necessária e suficiente para que dois planos sejam paralelos é que um deles contenha duas retas concorrentes, paralelas ao outro.
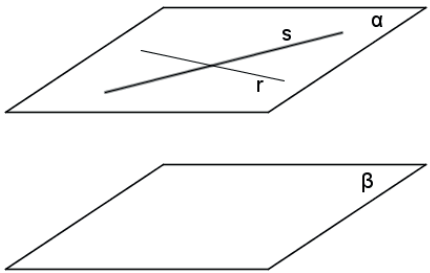

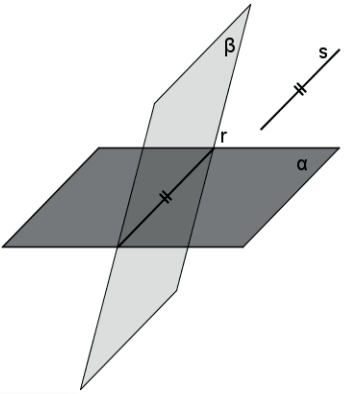
- Se dois planos são secantes e uma reta de um deles é paralela ao outro, então essa reta é paralela à interseção.
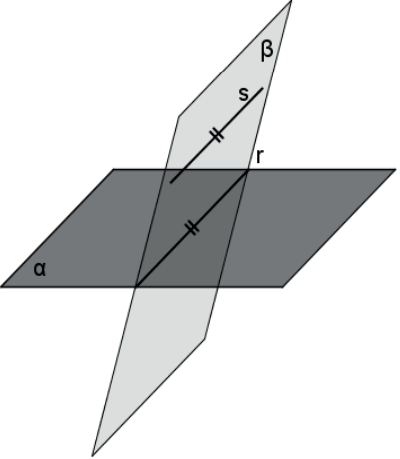

- Se duas retas distintas são paralelas entre si e um plano paralelo à primeira contém um ponto da segunda, então esse plano contém a segunda.
- Se uma reta é paralela a dois planos secantes, então ela é paralela à interseção desses planos.

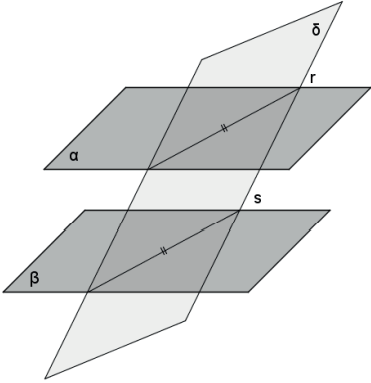
- Se dois planos são paralelos a um terceiro, então eles são paralelos entre si.
- Se dois planos paralelos entre si são interceptados por um terceiro, então as interseções são paralelas entre si.

PERPENDICULARIDADE
RETAS ORTOGONAIS
Ângulo entre retas reversas é o ângulo formado por duas retas concorrentes paralelas às retas dadas.
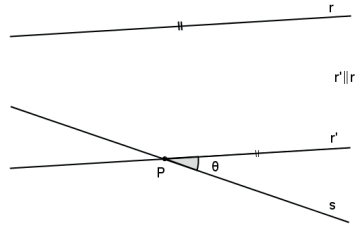
Retas ortogonais são retas reversas que formam ângulo reto.
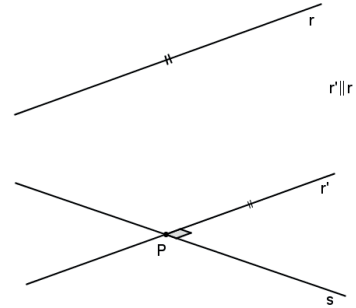
RETA E PLANO PERPENDICULARES
Uma reta e um plano são perpendiculares se, e somente se, a reta é perpendicular ou ortogonal a todas as retas do plano.
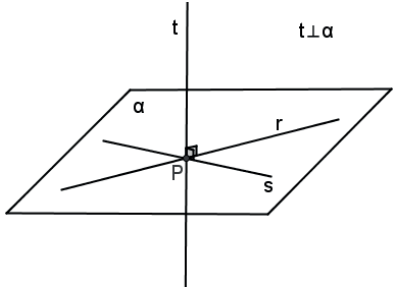
Se uma reta e um plano são perpendiculares, o traço (P) da reta no plano é o pé da perpendicular.
- Se uma reta é perpendicular a um plano, então ela é perpendicular ou ortogonal a qualquer reta do plano.
- Uma reta é perpendicular a um plano se, e somente se, é perpendicular (ou ortogonal) a duas retas concorrentes desse plano.
PLANOS PERPENDICULARES
- Um plano α é perpendicular a um plano β se, e somente se, α contém uma reta perpendicular a β.
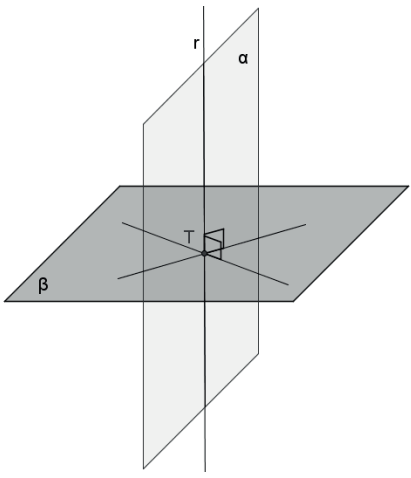

- Por uma reta r não perpendicular a um plano α, existe um único plano β perpendicular a α.
- Se dois planos são perpendiculares entre si e uma reta de um deles é perpendicular à interseção dos planos, então essa reta é perpendicular ao outro plano.
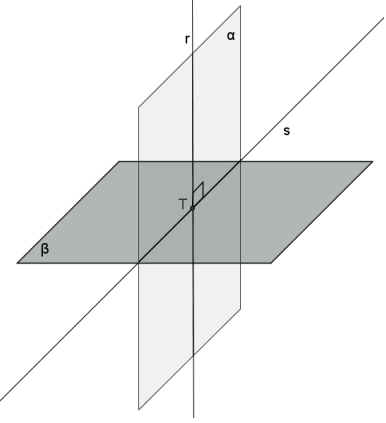

- Dois planos secantes são perpendiculares se, e somente se, toda reta de um deles, perpendicular à interseção, é perpendicular ao outro.
- Se uma reta é perpendicular a um plano, qualquer outro plano que a contenha é perpendicular ao primeiro.
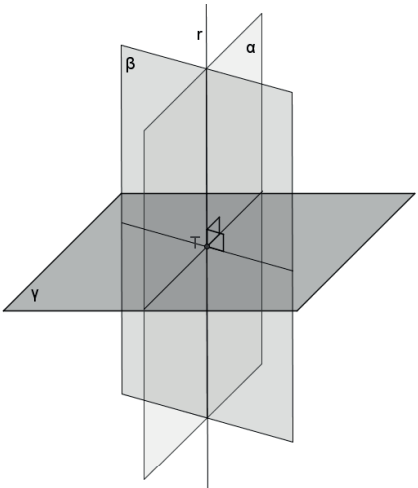
- Se um plano é perpendicular a dois planos secantes, então ele é perpendicular à interseção desses planos.

DISTÂNCIAS
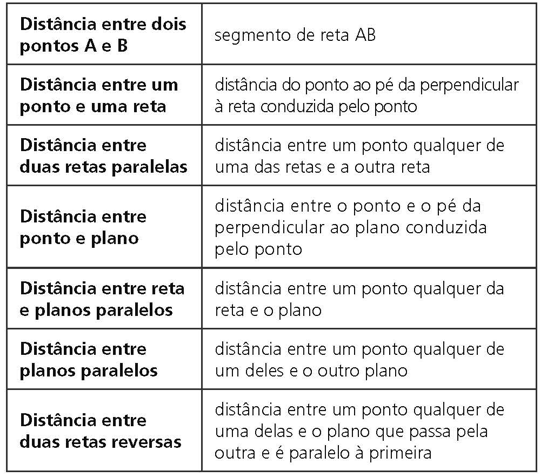
PERPENDICULAR COMUM: dadas duas retas reversas, existe uma única reta que é perpendicular comum a essas retas. De todos os segmentos que têm extremidades em cada uma das retas reversas, o menor é o da perpendicular comum.
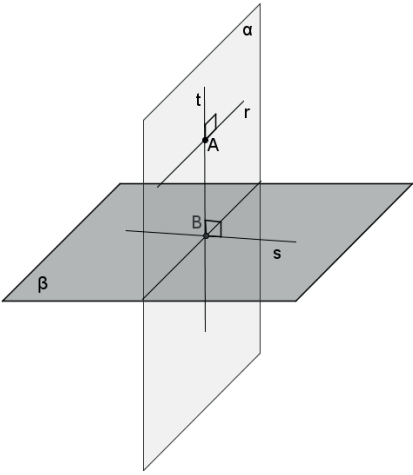
- Todo plano que passa pelo ponto médio de um segmento é equidistante das extremidades do segmento.
PROJEÇÃO ORTOGONAL
- Projeção ortogonal de um ponto sobre um plano: é o pé da perpendicular ao plano conduzida pelo ponto.
- Projeção ortogonal de uma figura sobre um plano: é o conjunto das projeções ortogonais dos pontos da figura sobre o plano.
- Projeção ortogonal de uma reta sobre um plano:
1°) reta perpendicular ao plano: traço da reta sobre o plano;
2°) reta não perpendicular ao plano: a projeção ortogonal da reta r sobre o plano α é o traço em α do plano β, perpendicular a α, conduzido por r.
α → plano de projeção
β → plano projetante
- Projeção ortogonal de um segmento de reta AB sobre um plano α, contido numa reta não perpendicular a esse plano é o segmento A’B’ de αα onde A’ e B’ são as projeções ortogonais de A e B, respectivamente, sobre o plano α.
ÂNGULO DE UMA RETA COM UM PLANO
- O ângulo entre uma reta e um plano oblíquos é o ângulo que a reta forma com sua projeção ortogonal sobre o plano.
- O ângulo entre uma reta e um plano perpendiculares é reto.
- Se a reta é paralela ou está contida no plano, o ângulo entre a reta e o plano é nulo.
- Se uma reta é oblíqua a um plano αα e o intercepta em A, então o ângulo agudo de r com sua projeção ortogonal r’ sobre α é menor que o ângulo agudo de r com qualquer outra reta de αα que passe por A.
- Se dois planos α e β são oblíquos, r é sua intersecção, e por um ponto P de α, não pertencente a r, são conduzidas duas retas concorrentes a e b, sendo a perpendicular a r, então o ângulo entre a reta α e β é maior que o ângulo entre a reta b e β.
- Reta de maior declive de um plano em relação a outro: se dois planos α e β são oblíquos, toda reta de α perpendicular à interseção dos planos é chamada reta de maior declive de α em relação a β. A reta de maior declive é a reta de αα que forma ângulo máximo com β.




