ÂNGULOS POLIÉDRICOS CONVEXOS
O conceito de ângulos poliédricos convexos é uma extensão do conceito de triedros. Dado um número finito n ≥ 3 de semirretas Va1, Va2,…Van, de mesma origem V, tais que o plano de duas consecutivas deixa as demais num mesmo semiespaço, consideremos n semiespaços E1, E2,…En cada um deles com origem no plano de duas semirretas consecutivas e contendo as restantes. Então o ângulo poliédrico convexo determinado por Va1, Va2,…Van, é a interseção dos semiespaços E1, E2,…En.
CONDIÇÃO DE EXISTÊNCIA
1) A medida de cada face está compreendida entre 0° e 180°.
2) Em todo ângulo poliédrico convexo, qualquer face é menor que a soma das demais
3) A soma das medidas das faces de um ângulo poliédrico convexo qualquer é menor que 360°.
POLIEDROS CONVEXOS E RELAÇÃO DE EULER
DEFINIÇÕES
Poliedro convexo é uma reunião de um número finito de polígonos planos convexos chamados faces onde:
1) dois polígonos não estão no mesmo plano;
2) cada lado de polígono é comum a dois e somente dois polígonos; e
3) o plano de cada polígono deixa os demais polígonos no mesmo semi-espaço.
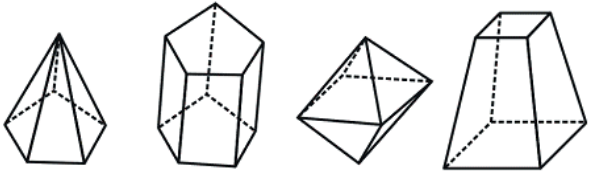
Os vértices das faces são também os vértices do poliedro e os lados das faces são chamadas arestas do poliedro.
Cada vértice do poliedro corresponde a um ângulo poliédrico, no qual está contido todo o poliedro.
- Diagonal do poliedro é qualquer segmento com extremidades em dois vértices do poliedro e não contido em uma face.
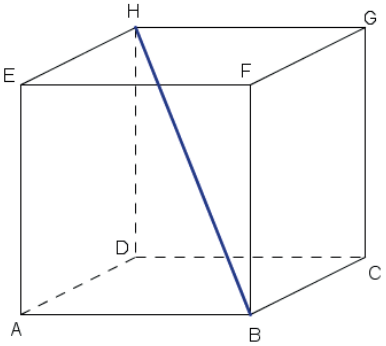
No poliedro acima, por exemplo, BH é uma diagonal.
Os poliedros são classificados de acordo com o seu número de faces.
O poliedro com menor número de faces é o tetraedro e possui 4 faces.
RELAÇÃO DE EULER
Seja um poliedro convexo com V vértices, A arestas e F faces, então
V + F = A + 2
Os poliedros que satisfazem a relação de Euler são chamados poliedros eulerianos.
Todo poliedro convexo é euleriano, mas nem todo poliedro euleriano é convexo.
A soma dos ângulos de todas as faces de um poliedro convexo de V vértices é
S = 360° · (V – 2)
Seja fn o número de faces de gênero n, então:
3f3+ 4f4 + … =2 A
Seja Vp o número de vértices onde concorrem p arestas, então:
3v3 + 4v4 +… = 2 A
Seja ∑df o total de diagonais das faces, então o número de diagonais do poliedro D é:
D = V(V-1)/2 – A – ∑df
POLIEDROS DE PLATÃO
Um poliedro é chamado poliedro de Platão se, e somente se,
- todas as faces têm o mesmo número de arestas;
- todos os ângulos poliédricos têm o mesmo número de arestas; e
- vale a relação de Euler (V-A+F=2).
Existem exatamente cinco poliedros de Platão.
Seja n o mesmo número de arestas de cada face e m o número de arestas dos ângulos poliédricos, temos:
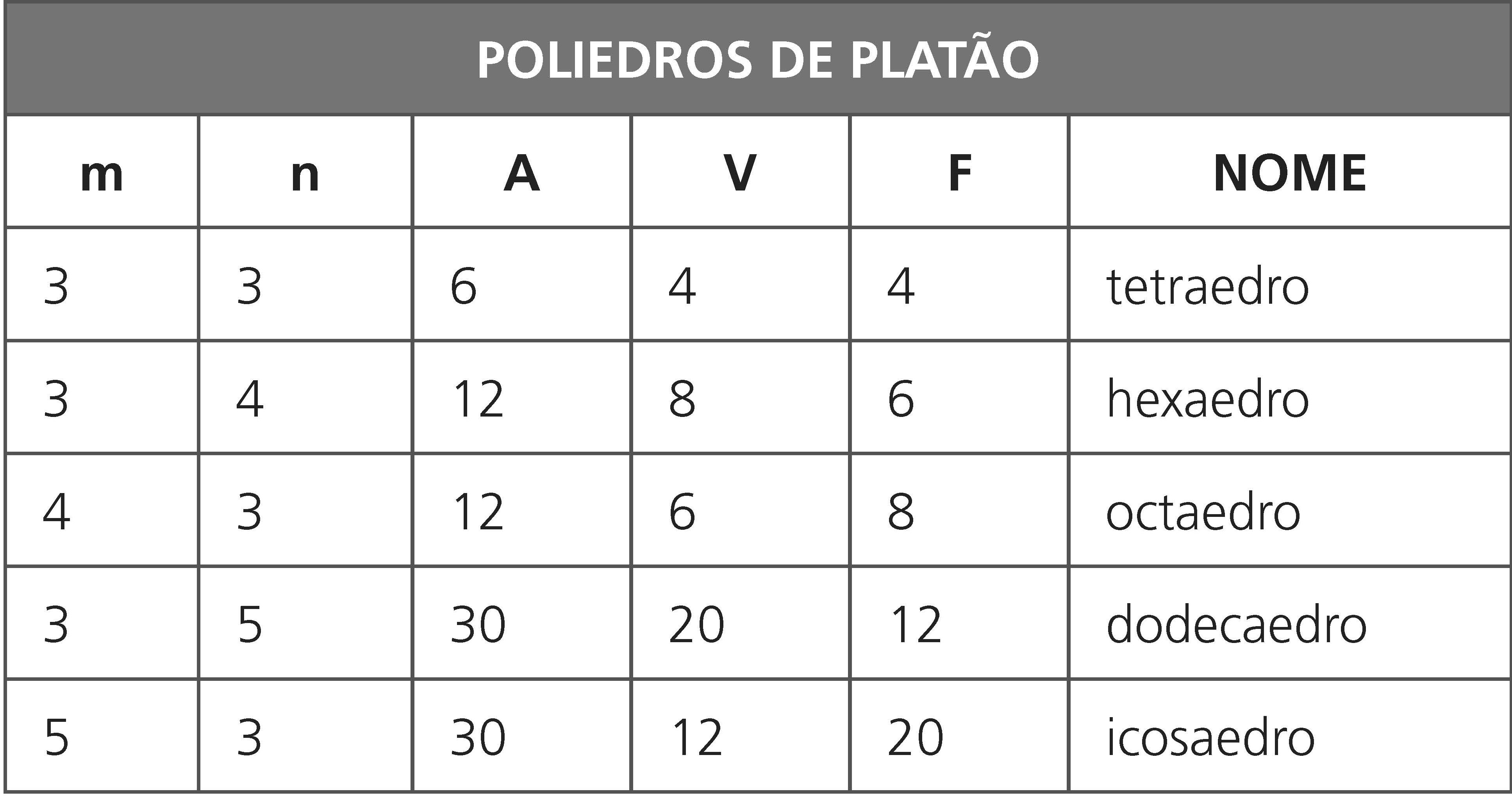
Um poliedro convexo é regular quando suas faces são polígonos regulares e congruentes e seus ângulos poliédricos são congruentes.
Todo poliedro regular convexo é um poliedro de Platão, mas nem todo poliedro de Platão é um poliedro regular.
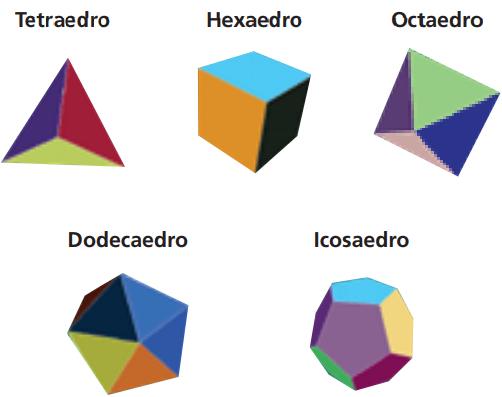
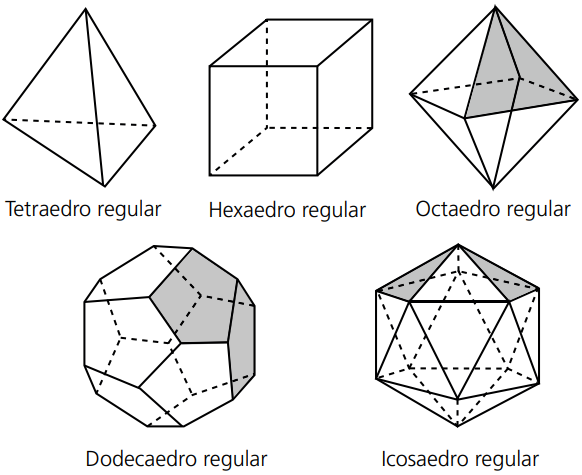
Os poliedros convexos regulares são cinco: o tetraedro regular, o hexaedro regular, o octaedro regular, o dodecaedro regular e o icosaedro regular.
TETRAEDRO REGULAR
- Quantidade de faces: 4
- Formato das faces: triângulos equiláteros
- Quantidade de vértices: 4
- Quantidade de arestas: 6
HEXAEDRO REGULAR
- Quantidade de faces: 6
- Formato das faces: quadrados
- Quantidade de vértices: 8
- Quantidade de arestas: 12
OCTAEDRO REGULAR
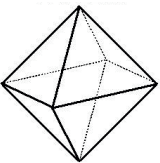
- Quantidade de faces: 8
- Formato das faces: triângulos equiláteros
- Quantidade de vértices: 6
- Quantidade de arestas: 12
DODECAEDRO REGULAR
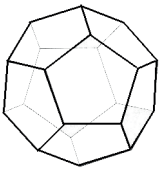
- Quantidade de faces: 12
- Formato das faces: pentágonos
- Quantidade de vértices: 20
- Quantidade de arestas: 30
ICOSAEDRO REGULAR
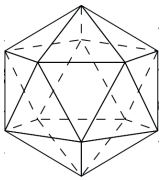
- Quantidade de faces: 20
- Formato das faces: triângulos equiláteros
- Quantidade de vértices: 12
- Quantidade de arestas: 30




