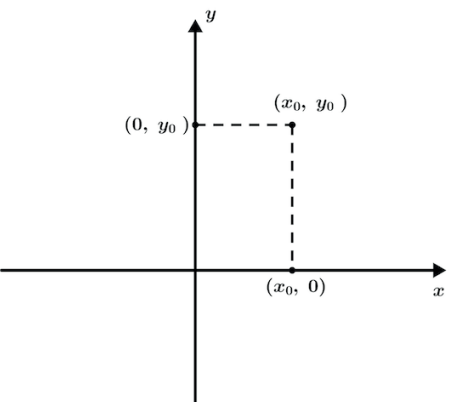
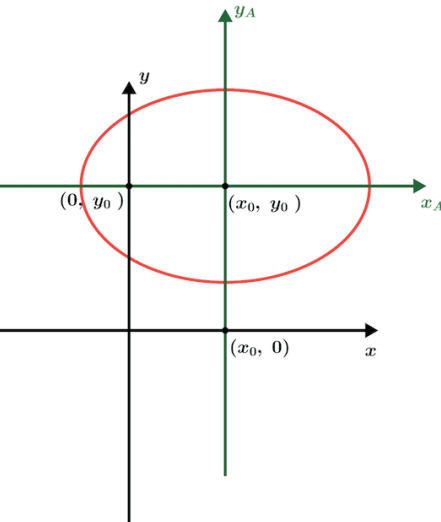
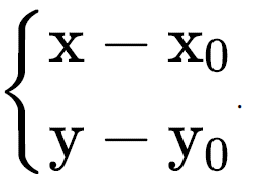Imagine que temos uma cônica que o centro não se encontra no centro (0,0) do nosso eixo cartesiano, mas sim possui centro no ponto (x0 , y0).
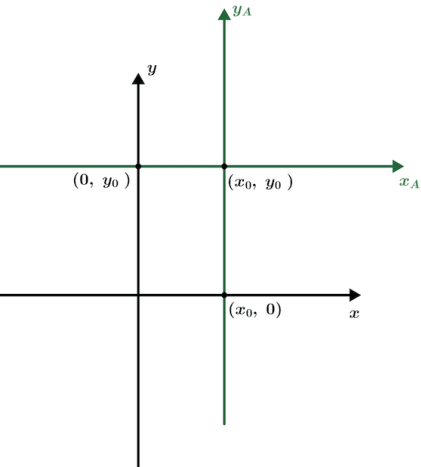
Sendo assim vamos criar os eixos cartesianos xA e yA que terá como centro o ponto (x0 ,y0).
Daí nós percebemos que se, a partir do plano cartesiano x · y, voltarmos x0 em x e voltarmos y0 em y estaremos novamente trabalhando com o centro do eixo cartesiano x · y. Sendo assim se tivermos por exemplo uma elipse com centro em (x0 , y0) esse será o centro do plano cartesiano xA · yA e para chegarmos no centro do plano cartesiano x · y teremos que fazer:
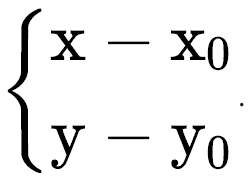
Assim para demonstrações podemos considerar qualquer centro (x0 ,y0) que sabemos que na verdade em relação a x · y teremos: