Geometria analítica plana: Ponto médio e distância

O ponto médio e a distância são conceitos cruciais na geometria analítica. O ponto médio de um segmento de reta é o ponto equidistante de seus extremos. A distância entre dois pontos é a medida do segmento de reta que os conecta. Essas noções são fundamentais para resolver problemas de posicionamento e cálculos em diversas aplicações, desde navegação até design de objetos.

PONTO MÉDIO E DISTÂNCIA

Vamos começar nossos estudos em apenas uma dimensão.

Vamos primeiramente definir distância em apenas uma dimensão.

Em um eixo, a distância entre x_A e x_B será x_B – x_A, o que chamamos de ponto final menos o ponto inicial. Sendo assim d_AB = x_B – x_A = ∆x.

Dessa forma podemos encontrar o ponto médio de um segmento.

Teremos que metade do segmento é ^xB−xA/₂ . Dessa forma a coordenada de x_M será x_A acrescida de ^xB−xA/₂ :

Assim para 2 dimensões, para o plano xy, basta fazermos o ponto médio em relação ao eixo x e o ponto médio em relação ao eixo y.

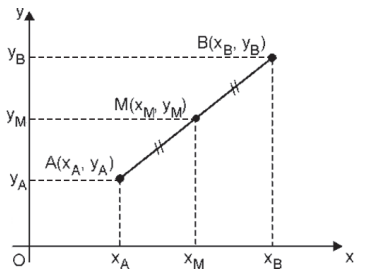
Assim o ponto médio M terá 2 coordenadas x_M e y_M.

Sendo M(x_M, y_M) o ponto médio do segmento cujas extremidades são A(x_A , y_A) e B(x_B , y_B), tem-se:

Para calcularmos a distância entre 2 pontos no plano xy basta observarmos a figura abaixo.

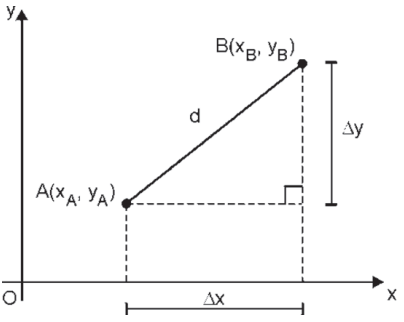
Temos a formação de um triângulo retângulo onde a hipotenusa é a distância entre os pontos A e B e os catetos são as distâncias em apenas uma dimensão, x_B – x_A = ∆x em relação ao eixo x e y_B – y_A = ∆y em relação ao eixo .

Sendo d a distância entre os pontos A(x_A , y_A) e B(x_B , y_B), aplicando o teorema de Pitágoras teremos: