O PLANO CARTESIANO
A cada ponto P do plano cartesiano corresponde um par ordenado (x, y) de números reais e escrevemos P(x, y) para indicar este ponto.
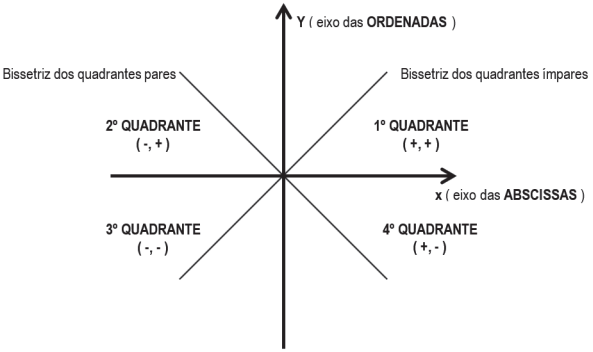
Dois eixos orientados (x e y) são dispostos ortogonalmente, dando a origem à divisão do plano em quatro partes, cada uma denominada quadrante. Os quatro quadrantes são numerados no sentido anti-horário, e os eixos e a intersecção entre eles são denominados, respectivamente, eixo das abscissas (x), eixo das ordenadas (y) e origem (0) do sistema de coordenadas cartesianas.
A reta que divide ao meio os quadrantes ímpares é chamada de bissetriz dos quadrantes ímpares e a que divide os quadrantes pares é a bissetriz dos quadrantes pares.
Qualquer ponto P no plano cartesiano terá coordenadas.
Se P ∈ ao 1ºquadrante: x > 0 e y > 0
Se P ∈ ao 2º quadrante: x < 0 e y > 0
Se P ∈ ao 3º quadrante: x < 0 e y < 0
Se P ∈ ao 4º quadrante: x > 0 e y < 0
A equação de reta da bissetriz dos quadrantes ímpares é x = y enquanto a equação da bissetriz dos quadrantes pares é x = –y.
Observações:
- Os pontos pertencentes ao eixo 0x↔ possuem ordenadas nulas.
P ∈ Ox → P = (x, 0)
- Os pontos pertencentes ao eixo 0y↔ possuem abscissas nulas.
P ∈ Oy → P = (0, y)
- Todos os pontos da bissetriz dos quadrantes ímpares possuem abscissas iguais à ordenada e vice-versa.
A ∈ bi → A = (a, a)
- Todos os pontos da bissetriz dos quadrantes pares possuem abscissas e ordenadas opostas e vice-versa.
B ∈ bp → B = (b, -b)
bi ⇒ bissetriz dos quadrantes ímpares
bp ⇒ bissetriz dos quadrantes pares




