OUTRAS EQUAÇÕES DE RETA
EQUAÇÃO COMPLETA DA RETA
Da equação reduzida y = mx + n quando isolamos todos os termos de um mesmo lado da igualdade passamos a ter os termos ax + by + c = 0 com a, b e c ∈ ℤ, que é a equação completa da reta.
Exemplo:

EQUAÇÃO SEGMENTÁRIA DA RETA
Da equação completa da reta ax + by + c = 0 isolaremos o termo c de um lado da igualdade, ax + by =–c e dividiremos todos os termos por -c, assim − a/c x − b/c y = 1.
Assim teremos por exemplo 2x − y − 6 = 0 e 2x − y − 6 = 0 ⇒ 2/6 x −1/6 y = 1⇒ x/3 − y/6 = 1.
Com a equação segmentária, podemos determinar os pontos de interseção da reta com os eixos ordenados do plano. O termo que divide x na equação segmentária é abscissa do ponto de intercessão da reta com o eixo x, e o termo que divide y é abscissa do ponto de interseção da reta com o eixo y. Assim:

EQUAÇÃO PARAMÉTRICA DA RETA
As equações paramétricas são duas equações que representam a mesma reta utilizando uma incógnita t. Essa incógnita recebe o nome de parâmetro e faz a ligação entre as duas equações que representam a mesma reta.
Vamos a um exemplo prático.
Seja a equação x − 2y + 3 = 0 → 2y = x + 3 → y = x+3/2. Vamos escolher uma parametrização arbitrária para y, por exemplo y = 2t + 1.
Assim sendo y = 2t + 1 e y = x+3/2 teremos que x+3/2 = 2t + 1→ x + 3 = 4t + 2 → x = 4t – 1.
Assim temos a equação paramétrica:

Para voltarmos para equação completa ou reduzida basta isolarmos

DISTÂNCIA DE PONTO A RETA
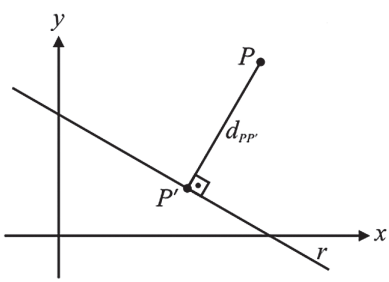
Sendo a equação da reta r : ax + by + c = 0 e P(x0, y0) temos:

Exemplo: A distância do ponto P(–1,1) a reta de equação y =−2x + 3 é

DISTÂNCIA ENTRE DUAS RETAS PARALELAS
Se r//s de equações r : ax + by + c1 = 0 e s : ax + by + c2 = 0





