HIPÉRBOLE
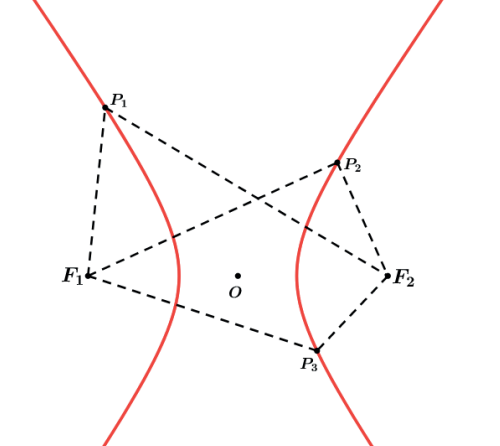
A hipérbole é o lugar geométrico dos pontos do plano cuja diferença das distâncias a 2 pontos fixos (focos) é sempre constante e igual a 2a (eixo real).
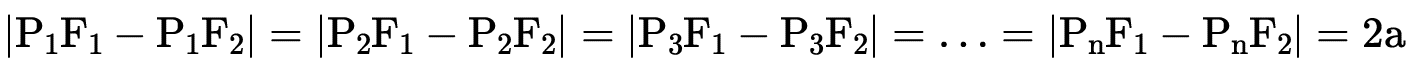
ELEMENTOS DA HIPÉRBOLE
Eixo real – O segmento que une os pontos mais próximos da hipérbole.
Distância focal – Distância entre os focos principais da hipérbole.
Eixo imaginário – Traçamos uma circunferência de centro no centro da hipérbole e raio igual a O̲F̲1. Por A1 traçamos uma perpendicular até que intercepte a circunferência, esse será o tamanho do eixo imaginário. O segmento paralelo passando pelo centro O será o eixo imaginário.
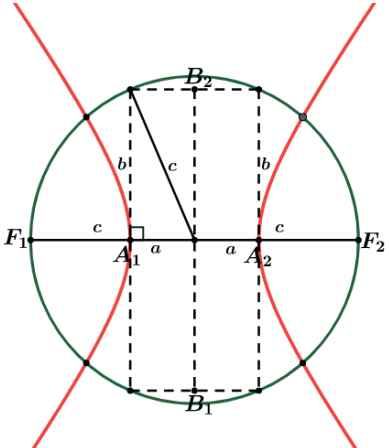
RELAÇÃO FUNDAMENTAL DA HIPÉRBOLE
Da figura que vemos os elementos da hipérbole percebemos que o raio da circunferência (c) será a hipotenusa do triângulo retângulo, dessa forma para a hipérbole nossa relação será
c² = a² + b²
EQUAÇÃO FUNDAMENTAL DA HIPÉRBOLE
Fazendo da mesma maneira que na elipse teremos a hipérbole centrada na origem (0, 0) e aplicaremos a definição P̲1̲F̲1̲ ̲- ̲P̲1̲F̲2̲ = 2a a partir de um ponto qualquer P(x, y).
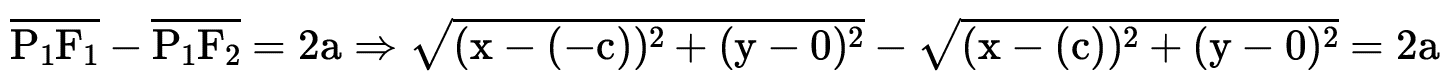
Deixo então o desenvolvimento para que seja feito por vocês da mesma maneira que na elipse, lembrando apenas que na hipérbole c2 = a2 + b2.
Depois de desenvolver nossa equação teremos:
Hipérbole centrada na origem de eixo real paralelo a Ox↔
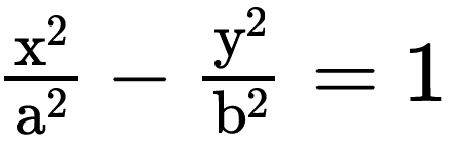
Hipérbole centrada na origem de eixo real paralelo a Oy↔
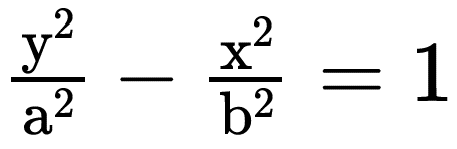
Fazendo a translação de eixos coordenados teremos as equações de hipérboles com centro em qualquer ponto.
Eixo real paralelo a Ox↔
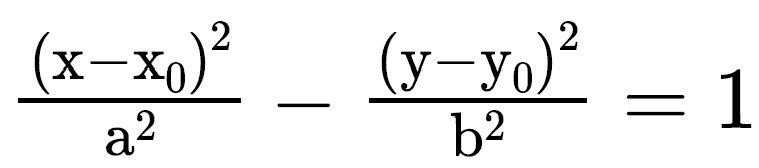
Eixo real paralelo a Oy↔
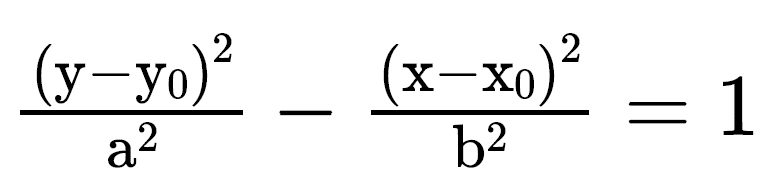
Na equação da hipérbole não devemos ter atenção quanto ao tamanho dos eixos, mas sim quanto aos sinais. Aquele que tiver o sinal positivo terá o eixo real e o que tiver sinal negativo terá o eixo imaginário. Dessa forma quando o sinal negativo “estiver no x” o eixo imaginário estará paralelo ao eixo x e quando o sinal negativo “estiver no y” o eixo imaginário estará paralelo ao eixo x, independente dos valores dos denominadores.
Hipérbole de eixo real paralelo a Ox↔
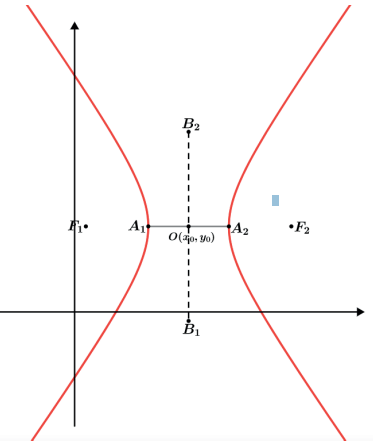
A1 = x0 − a
A2 = x0 + a
B1 = y0 − b
B2 = y0 + b
F1 = x0 − c
F2 = x0 + C
Hipérbole de eixo real paralelo a Oy↔
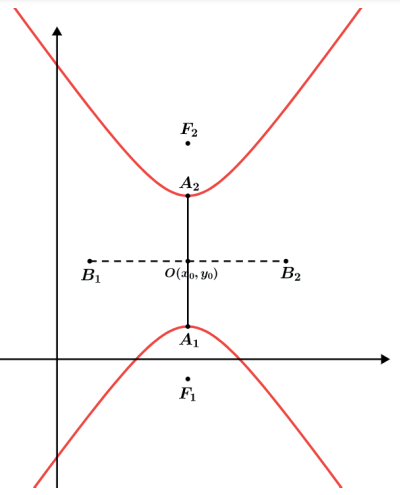
EQUAÇÃO COMPLETA
Temos por exemplo a equação da hipérbole (x−3)²/9 − (y+2)²/16 = 1 de onde podemos perceber que possui o centro em (3,−2) e a² = 9 ⇒ a = 3 e b² =16 ⇒ b = 4. Assim vemos que é uma hipérbole com eixo real paralelo a Ox↔. Vamos desenvolver a equação.
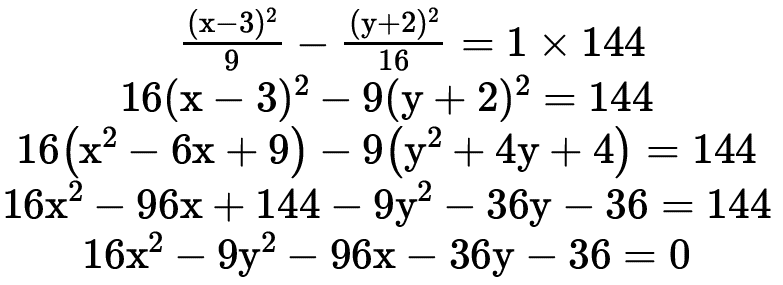
Assim ficamos com a equação que da forma que está não conseguimos identificar as coordenadas do centro ou os valores de a e de b.
Para chegarmos novamente à equação reduzida deveremos usar o mesmo artifício que utilizamos na equação da circunferência, completar quadrados.
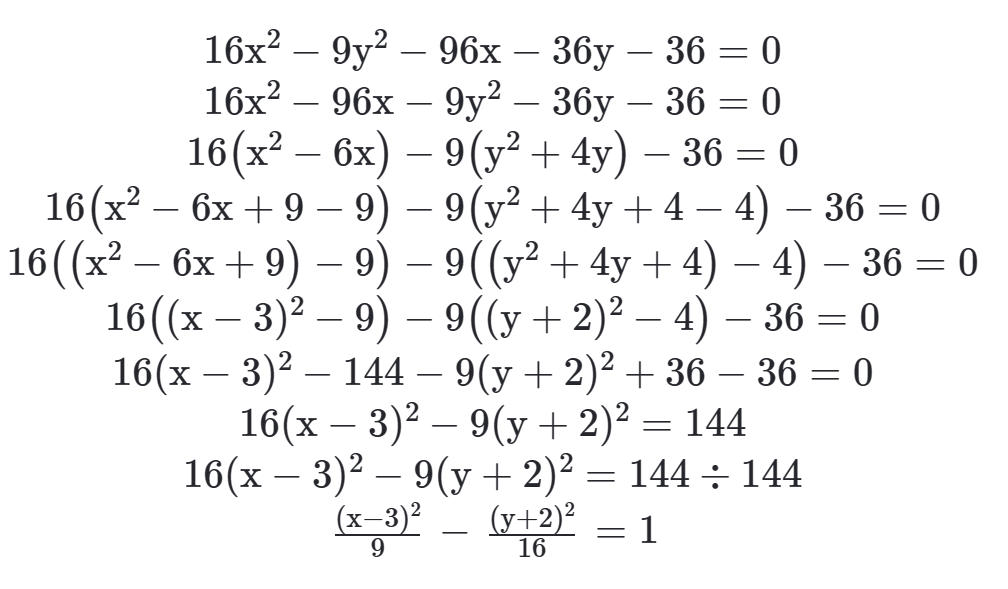
O processo é o mesmo da elipse, só devemos ter atenção com o sinal negativo, pois não deveremos subtrair o quadrado do segundo termo mas sim somar, como visto no processo (−9) · (−4)=36.
Assim nossa hipérbole será
c² = a² + b² ⇒ c² = 9 + 16 = 25 ⇒ c = 5
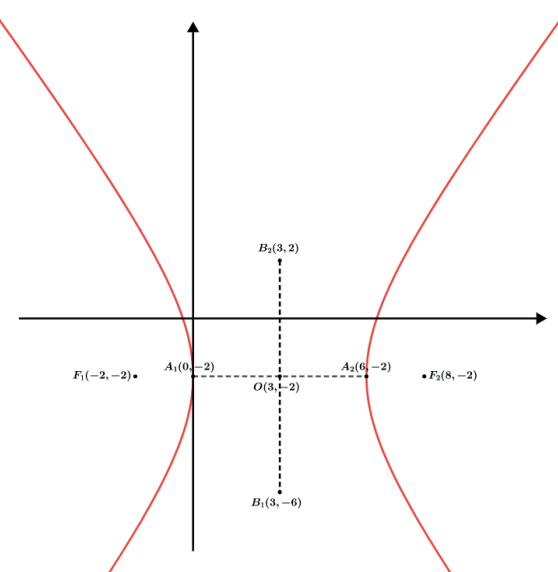
O(3, 2)
A1(0, −2)
A2(6, −2)
B1(3, −6)
B2(3, 2)
F1(−2, −2)
F2(8, −2)
HIPÉRBOLE EQUILÁTERA
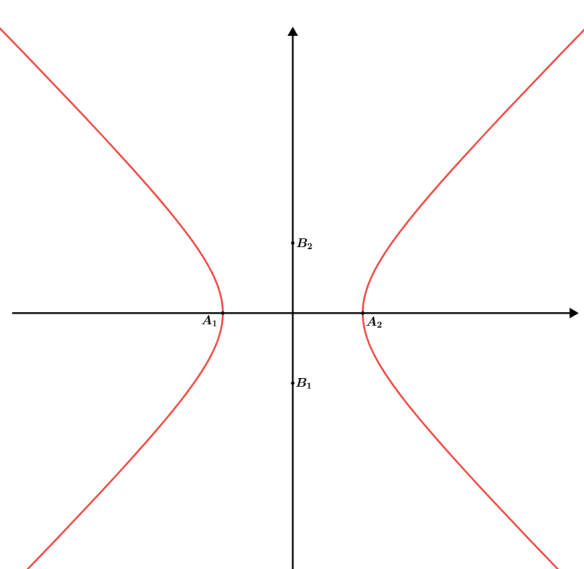
A hipérbole equilátera é aquela em que os eixos real e imaginário possuem as mesmas dimensões. Por exemplo x2 − y2 = 1 é um hipérbole equilátera pois x²/1 − y²/1 =1 e daí a² = b² = 1 ⇒ a = b = 1 e c² = a² + b² = 1 + 1 ⇒ c² = 2 ⇒ c = √2, assim temos A̲1̲A̲2̲ = B̲1̲B̲2̲.
EXCENTRICIDADE
A excentricidade mede o achatamento de uma cônica e é simbolizado por e, o seu cálculo se dá por e = c/a.
e = 1 → circunferência
e < 1 → elipse
e > 1 → hipérbole




