O CONJUNTO DOS REAIS POSITIVOS
Podemos fazer uma associação entre os pontos de uma reta orientada e o conjunto dos números reais. Essa reta é chamada de reta real.
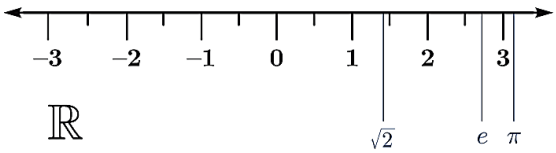
Ainda podemos dividir esta reta real em duas partes: os números menores que 0 (NEGATIVOS) e os números maiores que 0 (POSITIVOS). O conjunto dos reais positivos é denotado por ℝ*+ e o conjunto dos reais negativos é denotado por ℝ*– . Vejamos abaixo a propriedade fundamental acerca do conjunto dos reais positivos:
PROPRIEDADE: se x, y ∈ ℝ*+ então xy ∈ ℝ*+ e x + y ∈ ℝ*+. Em outras palavras, a soma de dois números positivos é positiva e o produto de dois números positivos é positivo.
MAIOR E MENOR
Dizemos que a > b se a diferença a – b pertence ao conjunto dos reais positivos, isto é, se a – b > 0. Uma outra maneira de escrever isto é que b < a.
Dizemos que a ≥ b se a = b ou a > b.
Vejamos alguns exemplos:
7 > 4
5 ≥ 3
3 ≥ 3
Observação: pensando na reta real, a > b significa que a está à direita de b.
PROPRIEDADES
TRANSITIVIDADE: se a > b e b > c, então a > c. (Isto é bem intuitivo pensando-se na reta real).
ADIÇÃO: se a > b e c > d, podemos somar as duas desigualdades: a + c > b + d.
Cuidado! Não podemos subtrair duas inequações! Veja o seguinte problema que isso nos causaria: 5 > 3 e 0 > –3. Se pudéssemos subtrair as inequações, chegaríamos a 5 – 0 > 3 – (– 3), ou seja, 5 > 6, o que é um absurdo! Então grava essa: NUNCA SUBTRAIA INEQUAÇÕES!
MULTIPLICAÇÃO POR UMA CONSTANTE: Se c é um número positivo e a > b, então ac > bc(VEJA QUE O SINAL INVERTE!).
Por exemplo, temos que 3 > 2. Ao multiplicar ambos os lados por –1, devemos inverter o sinal, obtendo –3 < –2.
Cuidado! Se chegarmos a uma situação como ac > bc, temos que analisar dois casos antes de cortar o c: se c for positivo, teremos a > b e se c for negativo, teremos a < b (MAIS UMA VEZ O SINAL INVERTE!). Fique bastante atento a isto!
INVERTENDO DESIGUALDADES: se a > b > 0, então 1/a < 1/b.
DESIGUALDADE BÁSICA: se x é um número real, então x2 ≥ 0. Estes conceitos de inequações serão muito úteis para módulos que virão pela frente! Guarde-os bem para não ser surpreendido lá na frente. Vamos enfrentar uma maratona de exercícios agora? Lute bastante com eles e não deixe de ver as soluções no final!




