TÉCNICA 1 (COLOCAR EM EVIDÊNCIA) – Quando um termo aparece em todas as parcelas de uma expressão algébrica, é possível colocar este em evidência. Matematicamente, temos o seguinte:
ab + ac = a(b + c)
Exemplo: x4 + x2y + xy2 = x(x3 + xy + y2)
TÉCNICA 2 (AGRUPAMENTO) – Esta técnica é muito utilizada e consiste na seguinte ideia:
ab + ac + bd + cd = a(b + c) + d(b + c) = (b + c)(a + d)
Veja que o agrupamento nada mais é que uma aplicação sucessiva da técnica de colocar em evidência.
Exemplo 1: x6 + x4 + x2 + 1 = x4(x2 + 1) + 1 · (x2 + 1) = (x2 + 1) (x4 + 1)
Exemplo 2: como consequência do agrupamento, podemos deduzir o chamado Produto de Stevin
x2 + (a + b)x + ab = x2 + ax + bx + ab = x(x + a) + b(x + a) = (x + a)(x + b).
FATORAÇÃO 1 (DIFERENÇA DE QUADRADOS) – Esta fatoração é a mesma coisa que o produto notável (PRODUTO DA SOMA PELA DIFERENÇA). Por sua grande importância, estamos ressaltando novamente:
a2 – b2 = (a + b)(a – b)
Exemplo:
x4 – 81 = (x2)2 – 92 = (x2 – 9) (x2 + 9) =
(x2 – 32) (x2 + 9) = (x – 3)(x + 3)(x2+9)
FATORAÇÃO 2 (SOMA DE CUBOS) – O objetivo aqui é fatorar a expressão a3 + b3. Lembre que vimos que (a + b)3 – a3 + b3 + 3ab(a + b). Como queremos fatorar a3 + b3, é natural isolar esta expressão de um dos lados da igualdade que vimos no ProBizu. Assim, temos que a3 + b3 – (a + b)3 – 3ab(a + b).
Colocando (a + b) em evidência, temos que: a3 + b3 = (a + b)((a + b)2 – 3ab) = (a + b)(a2 – ab + b2.)
Assim, chegamos à seguinte fatoração:
a3 + b3 = (a + b)(a2 – ab + b2)
Exemplo: x3 + 27 = x3 + 33 = (x + 3)(x2 – 3x + 9)
FATORAÇÃO 3 (DIFERENÇA DE CUBOS) – Agora, queremos fatorar a expressão a3 – b3. Para isso, vamos aproveitar a fatoração anterior:
a3 – b3 = a3 + (-b)3 = (a+(-b))(a2 – a · (-b) + (-b)2) = (a – b)(a2 + ab + b2)
Assim, temos:
a3 – b3 = (a – b)(a2 + ab + b2)
Exemplo: x3 – 64 = x3 – 43 = (x – 4)(x2 + 4x + 16)
FATORAÇÃO 4 (SOMA E DIFERENÇA DE POTÊNCIAS): Generalizando as duas últimas fatorações, temos os seguintes resultados um pouco mais avançados.
Para n inteiro positivo qualquer, vale:
xn – an = (x – a) (xn-1 + xn-2a + … + xan-2 + an-1)
Observe que as potências de x vão caindo de 1 em 1 e as de a vão aumentando de 1 em 1.
Exemplo:
x5 – 32 = x5 – 25 = (x – 2)(x4 + x3 · 2 + x2 · 22 + x · 23 + 24) =
(x – 2)(x4 + 2x3 + 4x2 + 8x + 16)
Para n inteiro positivo ÍMPAR, vale:
xn + an = (x + a)(xn-1 – xn-2 +…-xan-2 + an-1)
Observe que as potências de x vão caindo de 1 em 1 e as de a vão aumentando de 1 em 1. Além disso, repare também, que os sinais vão alternando.
Exemplo:
x5 + 32 = x5 + 25 = (x+2)(x4 – x3 · 2 + x2 · 22 – x · 23 + 24) =
(x + 2)(x4 – 2x3 + 4x2 – 8x + 16)
TÉCNICA 3 (COMPLETANDO QUADRADOS) – esta técnica é muito útil quando temos uma expressão que é quase um quadrado perfeito, mas não é. Vejamos dois exemplos para fixar as ideias.
Exemplos:
(Identidade de Sophie Germain) A expressão a ser fatorada é a4 + 4b4. Veja que a4 + 4b4 – (a2)2 + (2b2)2. Da forma que escrevemos, a expressão lembra muito o quadrado de uma soma (de fato já temos o quadrado do primeiro termo e o do segundo termo). Pense agora: o que está faltando para isto ser o quadrado de uma soma? Está faltando o termo do meio!! Para consertar isso, vamos somar e subtrair o termo do meio, que é 2 · a2 · (2b2) – 4a2b2. Assim, temos que:
a4 + 4b4 = a4 + 4a2b2 + 4b4 – 4a2b2 = (a2 + 2b2)2 – (2ab)2
Agora, temos uma diferença de quadrados e podemos fatorar nossa expressão, obtendo o seguinte:
a4 + 4b4 = (a2 + 2ab + 2b2)(a2 – 2ab + 2b2)
Vejamos mais um exemplo: (Identidade de Argand) A expressão a ser fatorada é x4 + x2 + 1. Você, ao olhar para esta expressão, deve ter pensado: “poxa, se em vez de x2, fosse 2x2, eu saberia fatorar como quadrado de uma soma!”. Você pensou muito bem e com este pensamento, podemos obter a fatoração. Se você quer que ali seja 2x2, basta somar e subtrair x2, obtendo assim: x4 + x2 + 1 = x4 + 2x2 + 1 -x2 = (x2+12) -x2. Mais uma vez, chegamos a uma diferença de quadrados e obtemos:
x4 +x2 + 1 = (x2 + x +1)(x2 – x +1)
TÉCNICA 4 (EXPRESSÕES DO SEGUNDO GRAU) – É bem possível que você se depare com expressões da forma ax2 + bx + c pela frente. Fique tranquilo: é bem fácil fatorar expressões deste tipo. Vejamos como:
1. Encontre as raízes x1 e x2 da equação ax2 + bx + c = 0 usando a fórmula de Bhaskara, por exemplo.
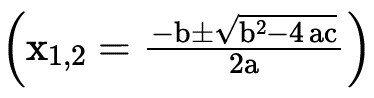
2. Feito isso, temos a seguinte fatoração: ax2 + bx + c = (ax – x1) (x – x2)
Vejamos um exemplo para fixar a ideia.
Exemplo: fatore 6x2 + x – 2.
Vamos seguir o passo a passo:
- As raízes são x1
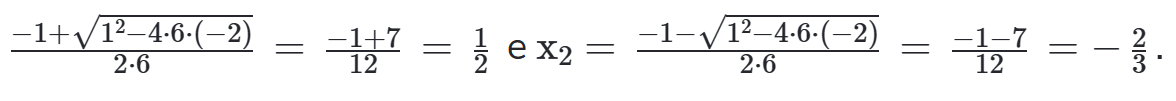
2. Desta forma, temos que:
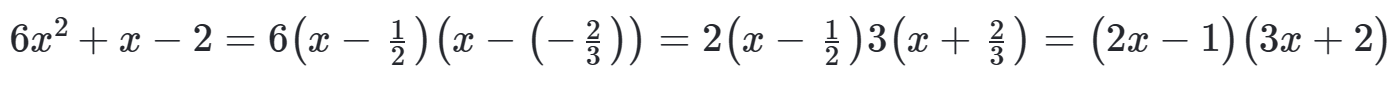
TÉCNICA 5 (ENCONTRANDO RAÍZES DE UMA EXPRESSÃO ALGÉBRICA): O seguinte resultado é extremamente útil: se uma expressão algébrica em x se anula para x = a, então x − a deve ser um fator da expressão.
Exemplo: fatore x3 – 6x2 + 11x – 6.
Veja que substituindo x por 1, temos que a expressão se anula. Desta forma, x−1 deve ser um fator. Sabendo desta informação, vamos buscá-lo com alguns artifícios:
x3 – 6x2 + 11x – 6 = x3 – x2 – 5x2 + 5x + 6x – 6=
x2(x – 1) – 5x(x – 1) + 6(x – 1) = (x – 1)(x2 – 5x + 6)
Ainda podemos fatorar x2 – 5x + 6 = (x – 2)(x – 3), obtendo assim que x3 – 6x2 + 11x – 6 = (x – 1)(x – 2)(x – 3).




