Seja P a imagem de um ângulo θ no ciclo trigonométrico. Já vimos que o seno do ângulo θθ é definido como a ordenada de P, ou seja, senθ = O̲P̲y¯. Assim, para obter o seno de θ, devemos projetar P sobre o eixo vertical Oy, denominado eixo dos senos.
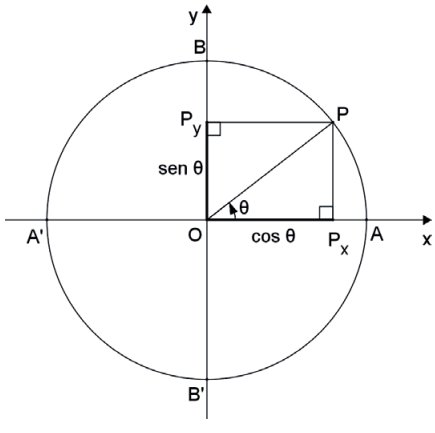
sen θ = O̲P̲y.
A função seno é a função de ℝ em ℝ definida por f(x)=sen x.
O domínio da função seno é Dsen = ℝ e a imagem Imsen=[-1,1].
A função seno é periódica de período 2π.
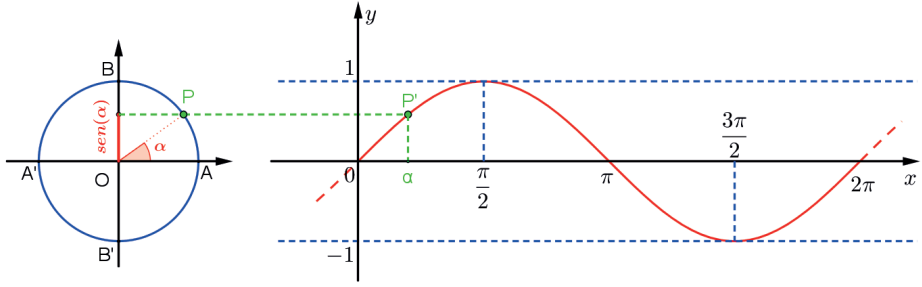
Vamos analisar o gráfico da função seno, estudando os valores do seno de um ângulo de 0 a π2π. Assim, observe o que acontece com o segmento orientado O̲P̲y conforme o ponto P dá uma volta no ciclo trigonométrico.
1º) De A até B, ou seja, de θ até θ = π/2, o seno cresce de f(0) = sen0 = 0 até f (π/2) = sen π/2 =1.
2º) De B até A, ou seja, de θ = π/2 até θ=π, o seno decresce de f (π/2) = sen π/2 =1 até f(π) = sen π=0.
3º) De A’ até B’, ou seja, de θ = π até θ= 3π/2, o seno decresce de f(π) = sen π = 0 até f (3π/2) = sen 3π/2 =-1.
4º) De B’ até A, ou seja, de θ = 3π/2 até θ = 2π, o seno cresce de f (3π/2) = sen 3π/2 = -1 até f(2π) = sen 2π = 0.